Частным случаем уравнения Лагранжа является уравнение Клеро.
Определение. Уравнение вида
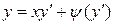 (16)
(16)
называется уравнением Клеро.
Уравнение Клеро отличается от уравнения Лагранжа только тем, что в нем коэффициент при 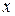 равен
равен 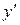 .
.
Решение уравнения. Применяем тот же метод, что и для интегрирования уравнения Лагранжа. Полагаем 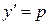 . Тогда уравнение (15) примет вид
. Тогда уравнение (15) примет вид
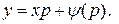 (17)
(17)
Дифференцируя по 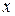 , получаем
, получаем
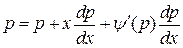 или
или 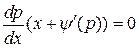 .
.
Это уравнение распадается на два: 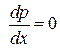 и
и 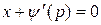 .
.
а) Из уравнения 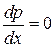 следует, что
следует, что 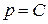 . Подставляя это значение
. Подставляя это значение 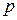 в
в
(17), получим
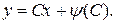 (18)
(18)
Это есть общее решение уравнения Клеро. Сравнивая (18) с (16), видим, что общее решение уравнения Клеро получается простой заменой в уравнении производной 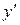 произвольной постоянной
произвольной постоянной 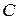 .
.
б) Из уравнения 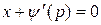 имеем
имеем 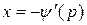 . Подставляя это значение
. Подставляя это значение 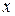 в (17), получаем
в (17), получаем 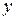 как функцию от параметра
как функцию от параметра 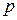 :
:
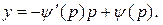
В результате имеем частное решение уравнения Клеро в параметрической форме
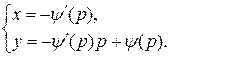
Это решение будет особым решением уравнения Клеро (см. §6 п. 6.2).
§5. Теоремы о существовании решения уравнения 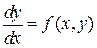
Мы познакомились с различными типами дифференциальных уравнений первого порядка, интегрируемых в квадратурах, были указаны методы их интегрирования. Однако рассмотренными уравнениями далеко не исчерпываются различные уравнения первого порядка. Уже более ста лет назад было доказано, что решение уравнений вида 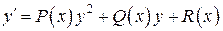 (уравнение Риккати) в общем случае не может быть выражено в квадратурах. Означает ли это, что уравнения не имеют решений? Можно доказать, что эти уравнения имеют решения, просто решения не могут быть выражены через элементарные функции или интегралы от элементарных функций. Оказывается, что таких уравнений, не интегрируемых в квадратурах, гораздо больше. Поэтому большое значение приобретают приближенные методы интегрирования дифференциальных уравнений. Однако, для того чтобы применять тот или иной метод приближенного интегрирования дифференциального уравнения, нужно прежде всего быть уверенным в существовании искомого решения, а так же и в единственности решения, так как при отсутствии единственности остается неясным, какое именно решение требуется приближенно определить. Поэтому фундаментальную роль в теории дифференциальных уравнений играют теоремы существования решений.
(уравнение Риккати) в общем случае не может быть выражено в квадратурах. Означает ли это, что уравнения не имеют решений? Можно доказать, что эти уравнения имеют решения, просто решения не могут быть выражены через элементарные функции или интегралы от элементарных функций. Оказывается, что таких уравнений, не интегрируемых в квадратурах, гораздо больше. Поэтому большое значение приобретают приближенные методы интегрирования дифференциальных уравнений. Однако, для того чтобы применять тот или иной метод приближенного интегрирования дифференциального уравнения, нужно прежде всего быть уверенным в существовании искомого решения, а так же и в единственности решения, так как при отсутствии единственности остается неясным, какое именно решение требуется приближенно определить. Поэтому фундаментальную роль в теории дифференциальных уравнений играют теоремы существования решений.
Приведем одну из теорем существования решения.
Теорема Пеано. Если правая часть уравнения
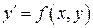 (1)
(1)
непрерывна в некоторой области 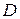 плоскости
плоскости 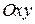 , то какова бы ни была внутренняя точка
, то какова бы ни была внутренняя точка 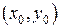 области
области 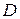 , в некоторой окрестности этой точки существует решение уравнения (1), удовлетворяющее условию
, в некоторой окрестности этой точки существует решение уравнения (1), удовлетворяющее условию 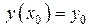 .
.
Заметим, что теорема Пеано единственности решения не гарантирует.
Докажем одну из основных теорем существования и единственности решения дифференциального уравнения (1).
Теорема Пикара. Пусть дано дифференциальное уравнение
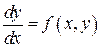 (1)
(1)
с начальным условием
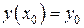 . (2)
. (2)
Если функция 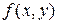 определена в прямоугольнике
определена в прямоугольнике
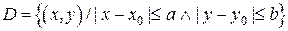 с центром в точке
с центром в точке 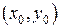 и удовлетворяет в этом прямоугольнике двум условиям:
и удовлетворяет в этом прямоугольнике двум условиям:
1) 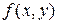 есть непрерывная функция двух переменных и поэтому ограниченная, то есть
есть непрерывная функция двух переменных и поэтому ограниченная, то есть
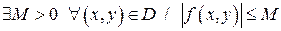 ; (3)
; (3)
2) функция 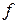 удовлетворяет условию Липшица по переменной
удовлетворяет условию Липшица по переменной 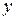 , то есть существует такое положительное число
, то есть существует такое положительное число 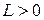 , что для двух любых точек
, что для двух любых точек 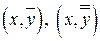 из прямоугольника
из прямоугольника 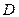 , отличающихся только ордината-
, отличающихся только ордината-
ми, выполняется неравенство
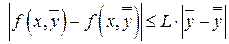 , (4)
, (4)
то уравнение (1) имеет единственное решение 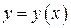 , удовлетворяющее
, удовлетворяющее
начальному условию (2), определенное и непрерывное на отрезке 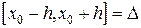 , где
, где 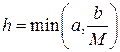 .
.
Это решение не выходит из прямоугольника 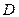 при
при 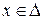 .
.
▲ Доказательство теоремы Пикара состоит из пяти этапов. Основная идея доказательства: задача Коши (1) - (2) сводится к некоторому интегральному уравнению, которое решается методом последовательных приближений Пикара, после чего доказывается, что найденное решение единственное.
1) Приведем задачу Коши к интегральному уравнению, то есть покажем, что решение уравнения (1) 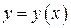 , удовлетворяющее начальному условию (2), будет являться решением интегрального уравнения
, удовлетворяющее начальному условию (2), будет являться решением интегрального уравнения
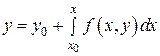 (5)
(5)
и наоборот.
а) Допустим, что 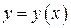 – решение дифференциального уравнения (1), удовлетворяющее начальному условию (2), определенное на отрезке
– решение дифференциального уравнения (1), удовлетворяющее начальному условию (2), определенное на отрезке  , график которого не выходит из прямоугольника
, график которого не выходит из прямоугольника 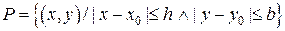 . Тогда должно выполняться тождество
. Тогда должно выполняться тождество
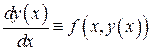 . (6)
. (6)
По условию теоремы 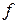 непрерывна в
непрерывна в 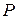 , а
, а 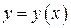 непрерывна на отрезке
непрерывна на отрезке  и график ее не выходит из прямоугольника
и график ее не выходит из прямоугольника 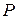 при
при 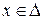 , тогда сложная функция
, тогда сложная функция 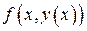 непрерывна на
непрерывна на  , поэтому данное равенство можно проинтегрировать на отрезке
, поэтому данное равенство можно проинтегрировать на отрезке 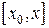 , где:
, где: 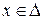 :
:
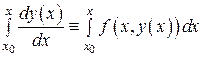 . (7)
. (7)
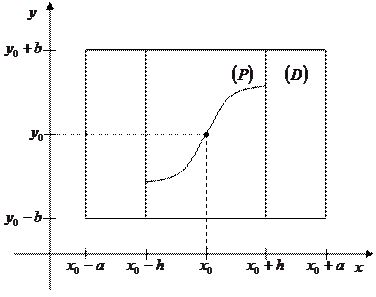
Рис. 8
Принимая во внимание начальное условие (2), получим
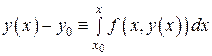
или
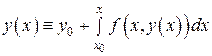 . (8)
. (8)
Сравнивая (5) и (8), заключаем, что 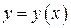 – решение интегрального уравнения (5).
– решение интегрального уравнения (5).
б) Пусть 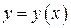 – решение интегрального уравнения (5), определенное и непрерывное на отрезке
– решение интегрального уравнения (5), определенное и непрерывное на отрезке  , график которого не выходит из прямоугольника
, график которого не выходит из прямоугольника 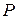 при
при 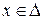 . Тогда имеем тождество (8). Как было отмечено выше,
. Тогда имеем тождество (8). Как было отмечено выше, 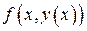 непрерывна на
непрерывна на  , поэтому интеграл в (8) можно дифференцировать по переменному верхнему пределу. Дифференцируя (8) по
, поэтому интеграл в (8) можно дифференцировать по переменному верхнему пределу. Дифференцируя (8) по 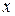 , получим тождество (6), следовательно,
, получим тождество (6), следовательно, 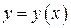 естьрешение уравнения (1).
естьрешение уравнения (1).
Полагая в тождестве (8) 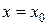 , получим
, получим
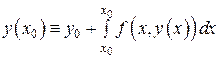 или
или 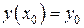 ,
,
то есть 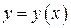 удовлетворяет начальному условию (2).
удовлетворяет начальному условию (2).
Итак, вместо того чтобы доказывать, что на некотором отрезке существует одно и только одно обращающееся в 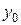 при
при 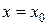 решение дифференциального уравнения (1) будем доказывать, что на этом отрезке существует одно и только одно непрерывное решение интегрального уравнения (5).
решение дифференциального уравнения (1) будем доказывать, что на этом отрезке существует одно и только одно непрерывное решение интегрального уравнения (5).
Будем искать решение уравнения (5) методом последовательных приближений Пикара. Этот метод состоит в том, что строится некоторая последовательность функций, сходящихся к искомому решению. Каждая из функций этой последовательности называется приближением к искомому решению.
2) Построим последовательность приближений к искомому решению на от-
резке  .
.
Сначала построим ее формально. В качестве нулевого приближения возьмем данное нам начальное значение 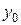 искомой функции
искомой функции
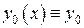 .
.
Геометрически это означает, что вместо искомого решения 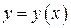 берется прямая
берется прямая 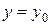 , проходящая через начальную точку (см. рис. 8). Подставляя в правую часть интегрального уравнения (5) вместо
, проходящая через начальную точку (см. рис. 8). Подставляя в правую часть интегрального уравнения (5) вместо 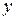 нулевое приближение, получим функцию
нулевое приближение, получим функцию 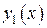 . Примем эту функцию за первое приближение:
. Примем эту функцию за первое приближение:
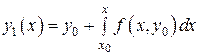 . (9)
. (9)
За второе приближение возьмем
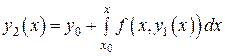 (10)
(10)
и т.д.; 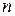 - е приближение
- е приближение 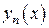 определим равенством
определим равенством
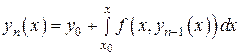 . (11)
. (11)
Продолжая этот процесс неограниченно, получим бесконечную последовательность функций
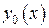 ,
, 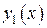 ,
, 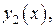
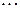 ,
, 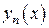
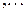 . (12)
. (12)
Докажем, что все функции последовательности (12) определены на отрезке  , непрерывны на нем и графики этих функций не выходят из прямоугольника
, непрерывны на нем и графики этих функций не выходят из прямоугольника 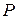 при
при 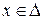 , то есть
, то есть
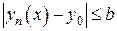 при
при 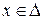 . (13)
. (13)
Очевидно, что 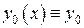 определена и непрерывна на
определена и непрерывна на  и график этой функции не выходит из прямоугольника
и график этой функции не выходит из прямоугольника 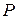 при
при 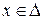 . Рассмотрим теперь функцию
. Рассмотрим теперь функцию 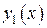 . Из (9) следует, что
. Из (9) следует, что 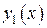 будет определена и непрерывна на
будет определена и непрерывна на  , если интеграл
, если интеграл 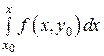 будет непрерывной функцией на отрезке
будет непрерывной функцией на отрезке  .
.
Рассмотрим подынтегральную функцию 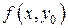 . По условию теоремы
. По условию теоремы 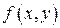 непрерывна по совокупности переменных в прямоугольнике
непрерывна по совокупности переменных в прямоугольнике 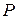 , а, следовательно, она непрерывна на отрезке
, а, следовательно, она непрерывна на отрезке  по переменной
по переменной 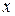 , поэтому функция
, поэтому функция 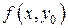 непрерывна на
непрерывна на  . Тогда в силу теоремы о непрерывности интеграла с переменным верхним пределом заключаем, что интеграл
. Тогда в силу теоремы о непрерывности интеграла с переменным верхним пределом заключаем, что интеграл 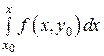 будет функцией непрерывной на
будет функцией непрерывной на  . Остается показать, что
. Остается показать, что 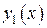 удовлетворяет условию
удовлетворяет условию
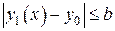 при
при 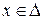 (14)
(14)
Из (9) имеем
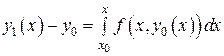 ,
,
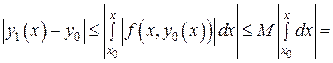
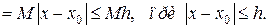 (15)
(15)
При оценке интеграла использовалось условие (3) теоремы. Действительно, когда 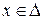 , точки
, точки 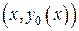
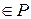 , тогда
, тогда 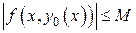 . Продолжая оценку (15), находим
. Продолжая оценку (15), находим
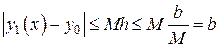 , (16)
, (16)
Следовательно, график функции 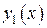 не выходит из прямоугольника
не выходит из прямоугольника 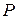 при
при 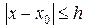 .
.
Пусть теперь доказываемое утверждение справедливо для 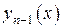 . Покажем, что тогда оно будет справедливо и для
. Покажем, что тогда оно будет справедливо и для 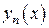 . Из (11) следует, что
. Из (11) следует, что 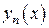 определена и непрерывна на
определена и непрерывна на  , если интеграл
, если интеграл 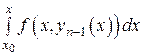 будет непрерывной функцией на отрезке
будет непрерывной функцией на отрезке  . Рассмотрим подынтегральную функцию
. Рассмотрим подынтегральную функцию 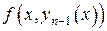 . По условию теоремы
. По условию теоремы 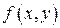 непрерывна по совокупности переменных в прямоугольнике
непрерывна по совокупности переменных в прямоугольнике 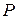 . По нашему допущению функция
. По нашему допущению функция 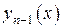 непрерывна на отрезке
непрерывна на отрезке  и график этой функции не выходит из прямоугольника
и график этой функции не выходит из прямоугольника 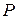 при
при 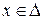 , то есть
, то есть
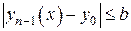 при
при 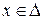 . (17)
. (17)
Тогда по теореме о непрерывности сложной функции функция 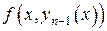 будет непрерывна на отрезке
будет непрерывна на отрезке  . В силу теоремы о непрерывности интеграла с переменным верхним пределом заключаем, что интеграл
. В силу теоремы о непрерывности интеграла с переменным верхним пределом заключаем, что интеграл 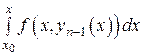
будет функцией непрерывной на  . Остается показать, что
. Остается показать, что 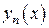 удовлетво-
удовлетво-
ряет условию
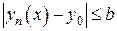 при
при 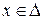 . (18)
. (18)
Из (11) имеем
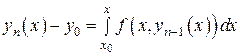 ,
,
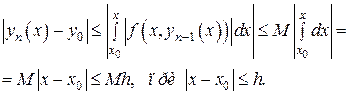 (19)
(19)
При оценке интеграла использовалось условие (3) теоремы. Действительно,
когда 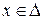 , точки
, точки 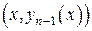
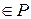 , тогда
, тогда 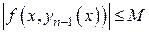 . Продолжая оценку (19), находим
. Продолжая оценку (19), находим
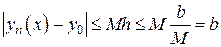 , (20)
, (20)
Следовательно, график функции 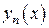 не выходит из прямоугольника
не выходит из прямоугольника  при
при 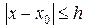 .
.
Так как для 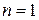 доказываемое утверждение справедливо, то из только что доказанного следует, что оно справедливо для всех
доказываемое утверждение справедливо, то из только что доказанного следует, что оно справедливо для всех 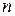 .
.
Итак, члены последовательности (12) определены и непрерывны на  и их графики не выходят из прямоугольника
и их графики не выходят из прямоугольника 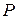 .
.
3) Докажем, что последовательность функций (12) сходится равномерно на
отрезке  .
.
Для доказательства рассмотрим функциональный ряд
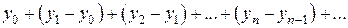 . (21)
. (21)
Его частичная сумма 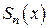 равна
равна
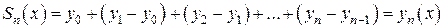 , (22)
, (22)
то есть общему члену последовательности (12). Тогда равномерная сходимость функциональной последовательности (12) будет означать равномерную сходимость последовательности частичных сумм ряда (21), а, следовательно, и равномерную сходимость ряда. Итак, достаточно доказать равномерную сходимость ряда (21) на отрезке  . Для этого воспользуемся признаком Вейерштрасса равномерной сходимости ряда. Чтобы построить для ряда
. Для этого воспользуемся признаком Вейерштрасса равномерной сходимости ряда. Чтобы построить для ряда
(21) мажорантный ряд, оценим члены этого ряда на отрезке  по модулю.
по модулю.
Для второго члена ряда имеем оценку (15):
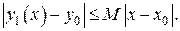 (23)
(23)
Оценим третий член ряда. Из (9) и (10) находим
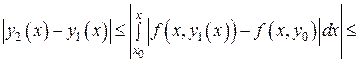
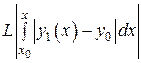 .
.
При оценке подынтегральной функции 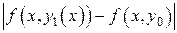 воспользовались условием Липшица (4). Это возможно, так как в первом пункте было до-
воспользовались условием Липшица (4). Это возможно, так как в первом пункте было до-
казано, что точки  ,
, 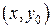 принадлежат прямоугольнику
принадлежат прямоугольнику 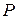 , когда
, когда 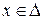 . Воспользовавшись оценкой (23), получим
. Воспользовавшись оценкой (23), получим
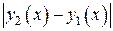
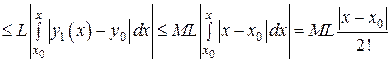 .
.
Аналогично рассуждая, для четвертого члена ряда находим оценку:
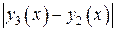
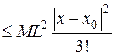
и т. д. Для общего члена ряда получим оценку:
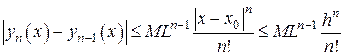 при
при 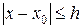 . (24)
. (24)
Самостоятельно убедитесь в справедливости оценки (24) методом математической индукции.
Рассмотрим числовой ряд, общим членом которого является правая часть неравенства (24):
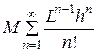 (25)
(25)
Данный ряд сходится при любом 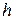 (убедитесь в этом, используя признак Да-
(убедитесь в этом, используя признак Да-
ламбера). В силу оценки (24) ряд (25) является мажорантным для ряда (21). Поэтому, согласно признаку Вейерштрасса, ряд (21) сходится на отрезке  равномерно к своей сумме, которую обозначим через
равномерно к своей сумме, которую обозначим через 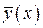 .Тогда, в силу неравенства (22) последовательность функций (12) сходится равномерно на отрезке
.Тогда, в силу неравенства (22) последовательность функций (12) сходится равномерно на отрезке  к своей предельной функции
к своей предельной функции 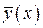 . Причем, по теореме о пределе равномерно сходящейся последовательности непрерывных функций предельная функция
. Причем, по теореме о пределе равномерно сходящейся последовательности непрерывных функций предельная функция 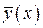 будет непрерывной на отрезке
будет непрерывной на отрезке  .
.
4) Докажем, что функция 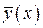 является решением интегрального уравнения (5) и, следовательно, является решением задачи Коши (1) - (2).
является решением интегрального уравнения (5) и, следовательно, является решением задачи Коши (1) - (2).
Покажем сначала, что график 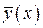 не выходит из прямоугольника
не выходит из прямоугольника 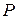 , когда
, когда 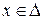 . Действительно, переходя к пределу в неравенстве (18), получим, что
. Действительно, переходя к пределу в неравенстве (18), получим, что 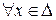
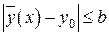 . Используя этот факт, такими же рассуждениями, как было доказано существование интеграла
. Используя этот факт, такими же рассуждениями, как было доказано существование интеграла 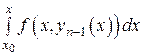 в пункте 2), можно доказать, что на отрезке
в пункте 2), можно доказать, что на отрезке  существует интеграл
существует интеграл 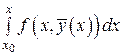 .
.
Докажем, что
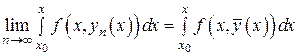 . (26)
. (26)
Для этого рассмотрим
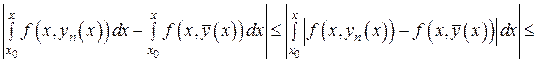
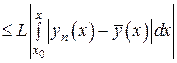
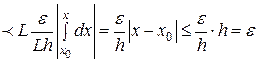 . (27)
. (27)
Сначала при оценке подынтегральной функции 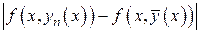 воспользовались условием Липшица (4). Это возможно, так как точки
воспользовались условием Липшица (4). Это возможно, так как точки  ,
,  принадлежат прямоугольнику
принадлежат прямоугольнику 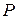 , когда
, когда 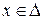 . Затем, оценивая
. Затем, оценивая 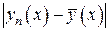 , пользуемся равномерной сходимостью последовательности
, пользуемся равномерной сходимостью последовательности 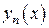 к функции
к функции 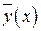 на отрезке
на отрезке  , которая означает, что
, которая означает, что
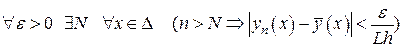 .
.
Таким образом имеем, что
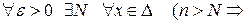
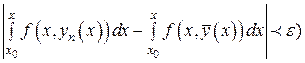 ,
,
откуда и следует (26).
Переходя теперь к пределу в равенстве
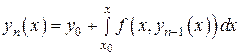
(см. п.1), получим тождество
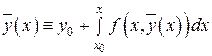 , (28)
, (28)
то есть функция 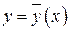 является решением интегрального уравнения (5) и, следовательно, решением дифференциального уравнения (1), удовлетворяющим начальному условию (2).
является решением интегрального уравнения (5) и, следовательно, решением дифференциального уравнения (1), удовлетворяющим начальному условию (2).
5 ) Докажем, что найденное решение единственно.
Предположим, что существует еще одно решение 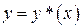 задачи Коши (1) - (2), определенное на
задачи Коши (1) - (2), определенное на  или
или 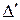 :
: 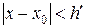 , где
, где 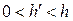 , которое обладает теми же свойствами: оно непрерывно на
, которое обладает теми же свойствами: оно непрерывно на 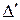 и его график не выходит из прямоугольника
и его график не выходит из прямоугольника 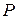 , то есть точки
, то есть точки 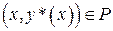 , когда
, когда 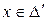 .
.
Без ограничения общности можно предположить, что значения 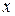 , для которых
, для которых 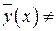
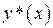 находятся вправо от точки
находятся вправо от точки 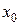 в любой близости от нее. В противном случае за точку
в любой близости от нее. В противном случае за точку 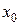 можно взять другую точку, в любой близости которой значения
можно взять другую точку, в любой близости которой значения 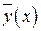 и
и 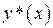 перестают быть равными. Пусть по предположению, на отрезке
перестают быть равными. Пусть по предположению, на отрезке 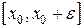 , где
, где 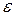 – некоторое малое положительное число, не всюду
– некоторое малое положительное число, не всюду 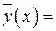
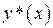 . Тогда положительная непрерывная функция
. Тогда положительная непрерывная функция 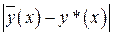 будет иметь на отрезке
будет иметь на отрезке 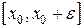 в некоторой точке
в некоторой точке 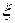 свое наибольшее значение
свое наибольшее значение 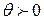 , причем
, причем 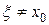 . Так как
. Так как 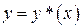 – решение интегрального уравнения, то имеем тождество
– решение интегрального уравнения, то имеем тождество
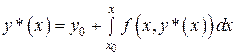 (29)
(29)
Вычтем из тождества (27) тождество (29), придавая 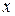 значение
значение 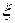 и используя при оценке разности условие Липшица:
и используя при оценке разности условие Липшица:
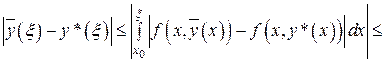
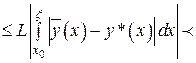
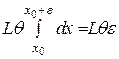 . (30)
. (30)
Последнее неравенство усилили, заменяя подынтегральную функцию ее наибольшим значением 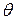 и распространяя интеграл на промежуток
и распространяя интеграл на промежуток 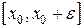 . Из (30) имеем неравенство
. Из (30) имеем неравенство 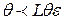 . Откуда
. Откуда 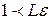 или
или 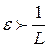 , что противоречиво, так как
, что противоречиво, так как 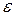 можно выбрать как угодно малым. Следовательно, допущение существования второго решения, удовлетворяющего тому же начальному условию, приводит к противоречию. ▲
можно выбрать как угодно малым. Следовательно, допущение существования второго решения, удовлетворяющего тому же начальному условию, приводит к противоречию. ▲
Сравнивая теорему Пикара и теорему Пеано, видим, что именно условие Липшица обеспечивает единственность решения.
Замечание 1 .(о продолжаемости решения)
Существование и единственность решения 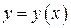 доказаны лишь на отрезке
доказаны лишь на отрезке 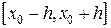 , однако, взяв точку
, однако, взяв точку 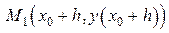 за начальную, можно, повторив рассуждения, продолжить решение еще на отрезок длины
за начальную, можно, повторив рассуждения, продолжить решение еще на отрезок длины 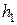 , если, в окрестности новой начальной точки выполнены условия теоремы Пикара. Действительно, предположим, что точка
, если, в окрестности новой начальной точки выполнены условия теоремы Пикара. Действительно, предположим, что точка 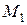 не лежит на границе прямоугольника
не лежит на границе прямоугольника 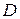 и рассмотрим прямоугольник
и рассмотрим прямоугольник 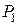 с центром в точке
с центром в точке 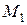 , содержащийся в
, содержащийся в 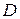 (рис.9). Примем точку
(рис.9). Примем точку 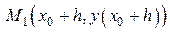 за начальную. В прямоугольнике
за начальную. В прямоугольнике 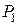 будут выполняться все условия теоремы, поэтому можно сделать вывод, что существует единственное решение
будут выполняться все условия теоремы, поэтому можно сделать вывод, что существует единственное решение 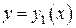 дифференциального уравнения, удовлетворяющее начальным условиям
дифференциального уравнения, удовлетворяющее начальным условиям
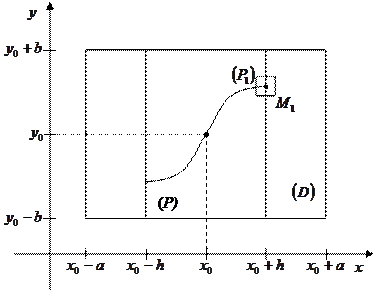
Рис. 9
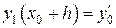 и определенное на отрезке
и определенное на отрезке 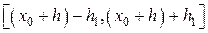 . Но на отрезке
. Но на отрезке 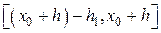 в силу единственности решения дифференциального уравнения
в силу единственности решения дифференциального уравнения 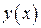 и
и 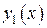 совпадают, поэтому
совпадают, поэтому 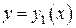 можно считать продолжением решения
можно считать продолжением решения 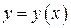 на отрезок
на отрезок 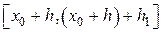 . Приняв за начальную точку конец
. Приняв за начальную точку конец 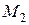 графика
графика 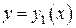 , решение можно продолжить дальше и т. д., пока не подойдем к границе области
, решение можно продолжить дальше и т. д., пока не подойдем к границе области 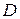 . Так же можно подойти к границе области
. Так же можно подойти к границе области 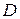 слева.
слева.
Замечание 2. Условие Липшица, которое на практике проверить трудно, можно заменить несколько более грубым, но легко проверяемым условием существования в области 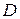 . ограниченной по модулю частной производной
. ограниченной по модулю частной производной 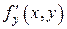
▲ Действительно, пусть в прямоугольнике 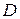 частная производная
частная производная 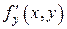 ограничена, то есть выполняется неравенство
ограничена, то есть выполняется неравенство
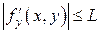 . (31)
. (31)
Применяя к функции 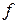 формулу Лагранжа о конечном приращении, получим
формулу Лагранжа о конечном приращении, получим
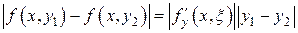 ,
,
где 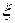 – промежуточное между
– промежуточное между 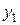 и
и 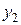 значение. Точка
значение. Точка 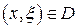 , поэтому, воспользовавшись условием (31),будем иметь
, поэтому, воспользовавшись условием (31),будем иметь
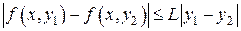 ,
,
то есть функция 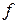 удовлетворяет условию Липшица относительно переменной
удовлетворяет условию Липшица относительно переменной 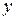 .
.
Заметим, что условие ограниченности производной 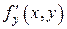 является только достаточным для выполнения условия Липшица. Подтвердим это примером. Для функции
является только достаточным для выполнения условия Липшица. Подтвердим это примером. Для функции 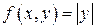 всегда имеет место неравенство
всегда имеет место неравенство
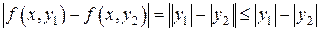 ,
,
то есть выполняется условие Липшица, в котором 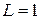 . Однако легко показать, что эта функция не имеет производной по
. Однако легко показать, что эта функция не имеет производной по 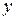 при
при 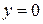 . ▲
. ▲
Замечание 3. Из теоремы Пикара и приведенных выше замечаний, будет следовать удобная для применения теорема Коши о существовании и единственности решения дифференциального уравнения (1).
Теорема Коши. Если функция 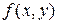 и ее частная производная
и ее частная производная 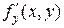 непрерывны в области
непрерывны в области 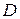 плоскости
плоскости 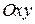 , то какова бы ни была внутренняя точка
, то какова бы ни была внутренняя точка 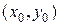 области
области 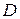 , в некоторой окрестности этой точки существует единственное решение
, в некоторой окрестности этой точки существует единственное решение 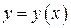 дифференциального уравнения
дифференциального уравнения
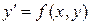 ,
,
удовлетворяющее начальному условию 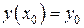 .
.
Геометрически это означает, что через каждую точку области 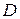 проходит единственная интегральная кривая.
проходит единственная интегральная кривая.
Действительно, если частная производная 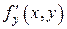 непрерывна в замкнутой области, то
непрерывна в замкнутой области, то 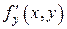 будет ограниченной по переменной
будет ограниченной по переменной 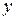 , тогда согласно замечанию 2 функция
, тогда согласно замечанию 2 функция 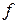 будет удовлетворять условию Липшица относительно переменной
будет удовлетворять условию Липшица относительно переменной 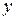 .
.
Замечание 4. Условия теоремы Коши являются достаточными для существования единственного решения, но не необходимыми, то есть через точку, в которой условия теоремы нарушаются, тем не менее, может проходить единственная интегральная кривая уравнения.
Пример 12. Для уравнения
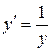
условия теоремы Коши в окрестности точек 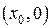 не выполнены, так как
не выполнены, так как 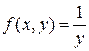 не является непрерывной, однако, через каждую такую точку проходит единственная интегральная кривая. Чтобы убедиться в этом, найдем общий интеграл уравнения в форме Коши:
не является непрерывной, однако, через каждую такую точку проходит единственная интегральная кривая. Чтобы убедиться в этом, найдем общий интеграл уравнения в форме Коши:
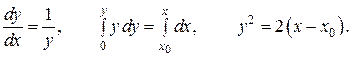
Видим, что через каждую точку 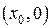 оси
оси 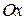 проходит единственная интегральная кривая (парабола). Особенность этих кривых состоит в том, что в точках
проходит единственная интегральная кривая (парабола). Особенность этих кривых состоит в том, что в точках 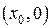 они имеют вертикальные касательные, так как
они имеют вертикальные касательные, так как 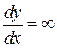 .
.
Применим теоремы существования к рассмотренным ранее дифференциальным уравнениям.
Пример 13. Доказать, что уравнение 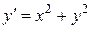 , которое не интегрируется в квадратурах, имеет единственное решение, удовлетворяющее любым начальным условиям
, которое не интегрируется в квадратурах, имеет единственное решение, удовлетворяющее любым начальным условиям 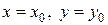 .
.
▲ Так как функция 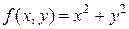 и ее частная производная
и ее частная производная 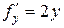 непрерывны на всей плоскости, то выполнены условия теоремы Коши и, следовательно, данное уравнение имеет единственное решение, удовлетворяющее рассматриваемому начальному условию. ▲
непрерывны на всей плоскости, то выполнены условия теоремы Коши и, следовательно, данное уравнение имеет единственное решение, удовлетворяющее рассматриваемому начальному условию. ▲
Пример 14. Выяснить вопрос о существовании и единственности решения, удовлетворяющего начальным условиям 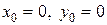 , для дифференциального уравнения
, для дифференциального уравнения 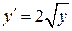 .
.
▲ Функция, стоящая в правой части уравнения, удовлетворяет условиям теоремы Пеано на всей плоскости, поэтому существует решение уравнения, удовлетворяющее начальным условиям 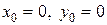 . Однако, эта функция в окрестности точки
. Однако, эта функция в окрестности точки 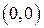 не удовлетворяет условиям теоремы Коши, так как
не удовлетворяет условиям теоремы Коши, так как 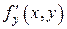 =
= 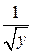 не ограничена в этой окрестности. Поэтому в этой точке может нарушатся единственность решения задачи Коши. Действительно, через точку
не ограничена в этой окрестности. Поэтому в этой точке может нарушатся единственность решения задачи Коши. Действительно, через точку 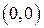 проходят две интегральные кривые этого дифференциального уравнения (см. §1, п.1.2). ▲
проходят две интегральные кривые этого дифференциального уравнения (см. §1, п.1.2). ▲
Замечание 5. Метод последовательных приближений, которым доказана теорема Пикара, является одновременно и эффективным методом приближенного интегрирования дифференциальных уравнений.
Пример 15. Найти третье приближение к решению уравнения
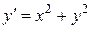
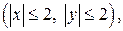 (32)
(32)
удовлетворяющего начальному условию 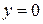 при
при 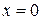 . (33)
. (33)
▲ Из теоремы Пикара следует, что существование единственного решения обеспечено на отрезке 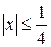 . Действительно, имеем:
. Действительно, имеем:
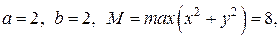 тогда
тогда 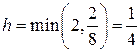 .
.
Заменим задачу Коши (32) - (33) равносильным ей интегральным уравнением
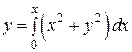 .
.
Находим три последовательных приближения, не считая 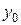 :
:
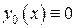 ,
, 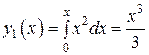 ,
,
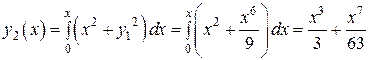 ,
,
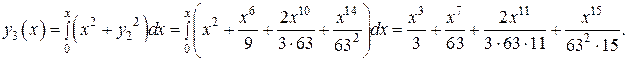 ▲
▲
 2015-03-22
2015-03-22 2332
2332








