Энергия системы заряженных тел

Рассмотрим систему 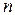заряженных тел. Используя закон сохранения энергии, можно показать, что потенциальная энергия 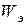системы заряженных тел

)

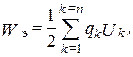где 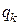, 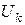- соответственно заряд и потенциал 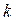- го тела (рис.2.8).

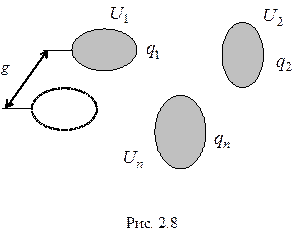
В качестве примера приведем соотношение для энергии системы, состоящей из двух разноименно заряженных тел (конденсатор). Имеем:

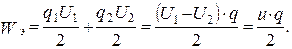
Известно, что 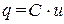, поэтому получим для конденсатора

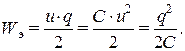
Энергия системы заряженных тел распределена в электрическом поле, окружающем заряженные тела. Введем понятие объемной плотности энергии электрического поля 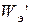([ 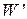] = Дж/м³)

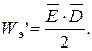
Для сред, в которых вектора 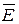и 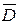совпадают по направлению (так называемые изотропные среды) справедливы равенства

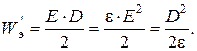
Полная энергия электрического поля в некотором объеме определится соотношением

(**)

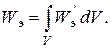При практическом определении величины 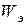выражения (*) и (**) равноценны, но последнее в большей степени отвечает физической сущности явления.