При наличии в линейной цепи одного или нескольких источников несинусоидальных периодических э.д.с. и токов расчет такой цепи выполняется в три этапа.
· Периодические несинусоидальные э.д.с. и токи источников раскладываются в ряд Фурье

· Расчет токов и напряжений в цепи производится для каждого из источников 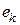 или
или 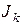 в отдельности.
в отдельности.
· Рассчитанные мгновенные значения токов 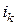 в рассматриваемой ветви суммируются
в рассматриваемой ветви суммируются
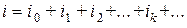 .
.
Первый этап расчета был изложен в предыдущем параграфе. Рассмотрим второй, наиболее трудоемкий, этап расчета.
При разложении периодической несинусоидальной э.д.с. 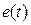 в ряд Фурье источник несинусоидальной э.д.с. можно рассматривать как последовательное соединение источника постоянной э.д.с.
в ряд Фурье источник несинусоидальной э.д.с. можно рассматривать как последовательное соединение источника постоянной э.д.с. 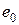 и источников синусоидальных э.д.с.
и источников синусоидальных э.д.с. 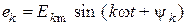 с частотами
с частотами 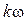 (
(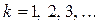 )
)

Источник периодического несинусоидального тока 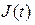 можно представить как параллельное соединение источника постоянного тока
можно представить как параллельное соединение источника постоянного тока 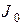 и источников синусоидального тока
и источников синусоидального тока 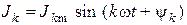 ,
, 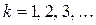
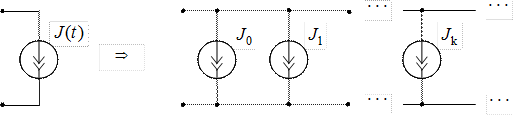
Применив метод наложения и рассмотрев действие каждого из источников э.д.с. 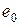 ,
, 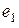 ,
, 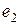 ,...,
,..., 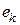 ,... (тока
,... (тока 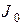 ,
, 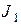 ,
, 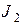 ,...,
,..., 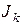 ,...) в отдельности можно найти составляющие
,...) в отдельности можно найти составляющие 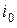 ,
, 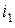 ,
, 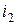 ,...,
,..., 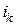 ,... искомых токов во всех ветвях цепи.
,... искомых токов во всех ветвях цепи.
Отметим, что при расчете составляющей тока 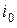 от действия постоянной э.д.с.
от действия постоянной э.д.с. 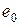 (источника постоянного тока
(источника постоянного тока 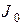 ) ветви с конденсаторами размыкаются, катушки индуктивности замыкаются накоротко, поскольку сопротивление конденсатора постоянному току бесконечно велико, а сопротивление катушки индуктивности равно нулю.
) ветви с конденсаторами размыкаются, катушки индуктивности замыкаются накоротко, поскольку сопротивление конденсатора постоянному току бесконечно велико, а сопротивление катушки индуктивности равно нулю.
При определении каждой из синусоидальных составляющих 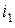 ,
, 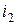 ,
, 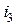 ...,
..., 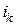 ,... искомого тока
,... искомого тока 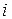 целесообразно воспользоваться комплексным методом расчета. Однако суммировать полученные комплексные токи для отдельных гармоник нельзя, так как они имеют разные частоты
целесообразно воспользоваться комплексным методом расчета. Однако суммировать полученные комплексные токи для отдельных гармоник нельзя, так как они имеют разные частоты 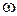 ,
, 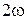 ,
, 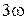 ,...,
,..., 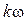 ,.... Необходимо суммировать мгновенные значения токов различных гармоник в той или иной ветви.
,.... Необходимо суммировать мгновенные значения токов различных гармоник в той или иной ветви.
При решении задачи определения каждой составляющей тока 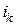 необходимо учитывать, что индуктивные и емкостные сопротивления зависят от частоты, различной для разных гармоник. Индуктивное сопротивление для
необходимо учитывать, что индуктивные и емкостные сопротивления зависят от частоты, различной для разных гармоник. Индуктивное сопротивление для 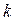 -ой гармоники в
-ой гармоники в 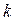 раз больше, чем для первой
раз больше, чем для первой
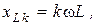
а емкостное сопротивление для 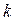 -ой гармоники в
-ой гармоники в 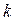 раз меньше, чем для первой
раз меньше, чем для первой
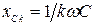
Определим ток 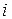 в цепи с последовательно соединенными элементами
в цепи с последовательно соединенными элементами 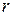 ,
, 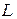 ,
, 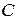 при действии периодического несинусоидального напряжения
при действии периодического несинусоидального напряжения 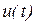 , разложенного в ряд Фурье.
, разложенного в ряд Фурье.
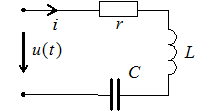
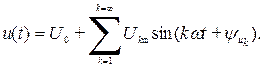
Считаем известными сопротивление резистора 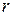 и сопротивления реактивных элементов
и сопротивления реактивных элементов 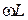 и
и 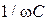 на частоте основной гармоники.
на частоте основной гармоники.
Искомый ток 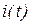 может быть представлен выражением вида:
может быть представлен выражением вида:
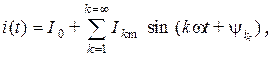
где определению подлежат величины 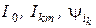 .
.
Постоянная составляющая тока в этой цепи равна нулю (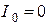 ), так как конденсатор не проводит постоянный ток.
), так как конденсатор не проводит постоянный ток.
Ток 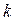 -ой гармоники рассчитаем комплексным методом. Можно записать
-ой гармоники рассчитаем комплексным методом. Можно записать
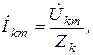 где
где 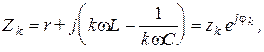
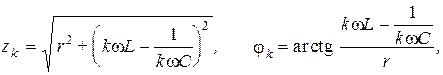
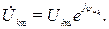
Тогда
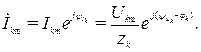
Окончательно получим:
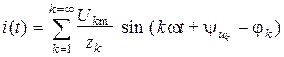
Отметим, что 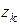 и
и 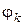 зависят от порядка
зависят от порядка 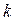 гармоники, поэтому при любых значениях параметров
гармоники, поэтому при любых значениях параметров 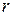 ,
, 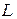 ,
, 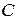 форма кривой тока
форма кривой тока 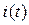 не будет подобна форме кривой приложенного напряжения
не будет подобна форме кривой приложенного напряжения 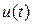 .
.
 2015-03-22
2015-03-22 341
341








