Если первичные параметры линии 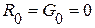 , то она называется линией без потерь (рис. 4). Такая идеализация справедлива для коротких по длине линий, работающих на сверхвысоких частотах (фидеров, элементов
, то она называется линией без потерь (рис. 4). Такая идеализация справедлива для коротких по длине линий, работающих на сверхвысоких частотах (фидеров, элементов 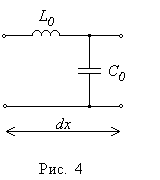 радиотехнических устройств, полосковых линий, согласующих СВЧ устройств и других), где выполняются условия
радиотехнических устройств, полосковых линий, согласующих СВЧ устройств и других), где выполняются условия 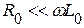 и
и 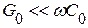 , и резистивными сопротивлением и проводимостью можно пренебречь по сравнению с сопротивлением индуктивности и проводимостью ёмкости в линии.
, и резистивными сопротивлением и проводимостью можно пренебречь по сравнению с сопротивлением индуктивности и проводимостью ёмкости в линии.
Коэффициент распространения линии без потерь:
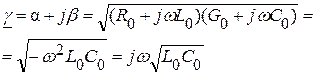 ,
,
и условия (6.1), (6.2) выполняются: коэффициент ослабления амплитуды 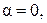 а коэффициент фазы
а коэффициент фазы 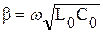 линейно зависит от частоты, при этом фазовая скорость
линейно зависит от частоты, при этом фазовая скорость 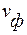 равна постоянной величине
равна постоянной величине 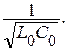 Линия без потерь не вносит амплитудно-частотных и фазочастотных искажений в передаваемый сигнал.
Линия без потерь не вносит амплитудно-частотных и фазочастотных искажений в передаваемый сигнал.
Волновое сопротивление линии без потерь 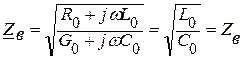 является резистивным.
является резистивным.
Уравнения передачи (2.10 б) для линии без потерь с учётом 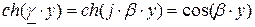 и
и 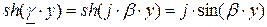 принимают вид:
принимают вид:
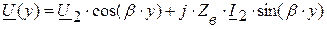 (7.1)
(7.1)
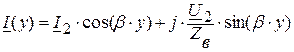 (7.2)
(7.2)
Входное сопротивление линии без потерь, согласно (5.1),
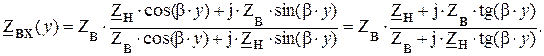 (7.3)
(7.3)
С учётом 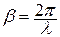
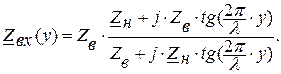 (7.4)
(7.4)
В зависимости от нагрузки 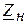 на конце линии различают следующие режимы работы:
на конце линии различают следующие режимы работы:
- линия с разомкнутыми выходными зажимами 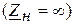 ,
,
- линия с замкнутыми накоротко выходными зажимами 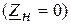 ,
,
- подключение к линии реактивной нагрузки 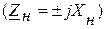 ,
,
- подключение к линии согласованной нагрузки 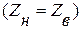 ,
,
- подключение к линии несогласованной нагрузки 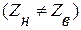 .
.
Рассмотрим распределение напряжения и тока вдоль линии при различных режимах работы. Уравнения передачи линии без потерь (7.1), (7.2) с учётом 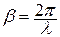 имеют вид:
имеют вид:
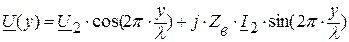 (7.5)
(7.5)
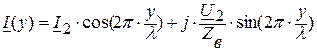 , (7.6)
, (7.6)
где 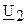 ,
, 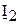 - комплексные значения напряжения и тока в конце линии (то есть в нагрузке);
- комплексные значения напряжения и тока в конце линии (то есть в нагрузке); 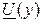 ,
, 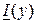 - комплексные значения напряжения и тока на расстоянии у от конца линии.
- комплексные значения напряжения и тока на расстоянии у от конца линии.
 7.1. В режиме холостого хода, то есть когда линия на конце разомкнута
7.1. В режиме холостого хода, то есть когда линия на конце разомкнута 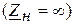 ,
, 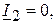 уравнения (7.5), (7.6) преобразуются в:
уравнения (7.5), (7.6) преобразуются в:
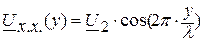 (7.7)
(7.7)
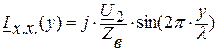 . (7.8)
. (7.8)
Если начальную фазу напряжения 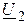 принять равной нулю (
принять равной нулю (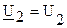 ,
, 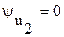 ), тогда мгновенные значения напряжения и тока:
), тогда мгновенные значения напряжения и тока:
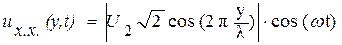 (7.9)
(7.9)
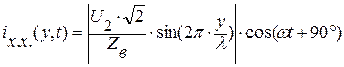 (7.10)
(7.10)
Действующие значения напряжения и тока в 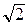 раз меньше амплитудных и соответственно определяются из выражений:
раз меньше амплитудных и соответственно определяются из выражений:
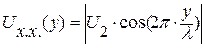 (7.11)
(7.11) 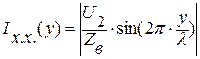 (7.12)
(7.12)
В выражения (7.11), (7.12) переменная времени не входит, следовательно, распределение действующих значений напряжения и тока вдоль линии с течением времени не меняется. Рассмотренный режим колебаний называют режимом стоячих волн.
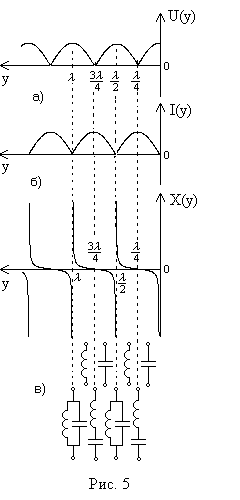
На рисунках 5.а и 5.б показано распределение действующих значений напряжения и тока вдоль линии. В линии имеются точки, где амплитуда колебаний равна нулю (узлы напряжения или тока) и точки, где амплитуда колебаний максимальна (пучности напряжения или тока). Стоячие волны являются результатом сложения падающей и отражённой волн с равными амплитудами (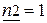 ). В пучностях фазы обеих волн совпадают и амплитуда суммарной волны вдвое больше амплитуды падающей волны, а в узлах фазы противоположны и амплитуда суммарной волны равна нулю.
). В пучностях фазы обеих волн совпадают и амплитуда суммарной волны вдвое больше амплитуды падающей волны, а в узлах фазы противоположны и амплитуда суммарной волны равна нулю.
Условия возникновения стоячей волны могут быть сформулированы так:
1. α = 0 дБ/м – линия без потерь;
2. |n2| = 1, или Рн = U2·I2·cos(φz) = 0 – полное отражение падающей волны от выходных зажимов линии.
При этом U(y) и I(y) - распределения вдоль линии значений амплитуд колебаний, - определяются законами синус или косинус; а фазы этих колебаний от координаты «у» не зависят.
Входное сопротивление разомкнутой линии в режиме холостого хода на расстоянии «у» от выходных зажимов:
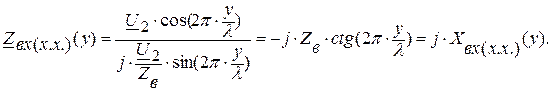 (7.13)
(7.13)
График зависимости Хвх(х.х.)(у) представлен на рисунке 5.в.
Разомкнутая на конце линия длиной от 0 до 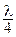 имеет входное сопротивление емкостного характера (Хвх(х.х.) < 0).
имеет входное сопротивление емкостного характера (Хвх(х.х.) < 0).
Линия длиной 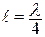 имеет входное сопротивление равное 0, то есть такой отрезок длинной линии аналогичен последовательному колебательному контуру без потерь (Хвх(х.х.) = 0).
имеет входное сопротивление равное 0, то есть такой отрезок длинной линии аналогичен последовательному колебательному контуру без потерь (Хвх(х.х.) = 0).
Линия длиной от 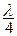 до
до 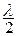 имеет входное сопротивление индуктивного характера (Хвх(х.х.) > 0).
имеет входное сопротивление индуктивного характера (Хвх(х.х.) > 0).
Линия длиной 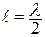 имеет неограниченно большое входное сопротивление (Хвх(х.х.) = ∞), то есть такой отрезок длинной линии аналогичен параллельному колебательному контуру без потерь.
имеет неограниченно большое входное сопротивление (Хвх(х.х.) = ∞), то есть такой отрезок длинной линии аналогичен параллельному колебательному контуру без потерь.
7.2. В режиме короткого замыкания, то есть когда линия на конце замкнута 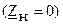 ,
, 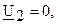 уравнения (7.1), (7.2), (7.3) преобразуются:
уравнения (7.1), (7.2), (7.3) преобразуются:
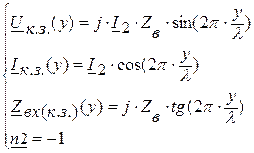 (7.14)
(7.14)
Если начальную фазу тока I 2 принять равной нулю, тогда мгновенные значения напряжения и тока:
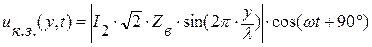
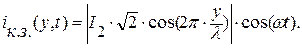 (7.15)
(7.15)
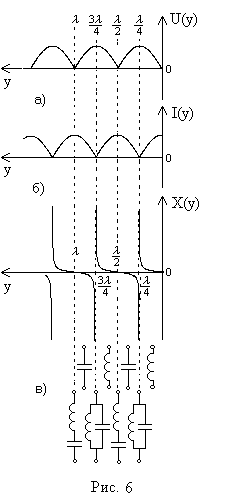
Графики распределения амплитудных значений напряжения и тока, а также и входного сопротивления, вдоль линии показаны на рисунках 6.(а, б, в). В короткозамкнутой линии, также как и в разомкнутой, имеет место режим стоячих волн.
Короткозамкнутая линия без потерь длиной 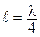 имеет неограниченно большое входное сопротивление (Xвх(к.з.) = ∞). Если в линии имеются потери, то входное сопротивление не бесконечно, но достаточно велико. Это свойство используется в схемотехнике.
имеет неограниченно большое входное сопротивление (Xвх(к.з.) = ∞). Если в линии имеются потери, то входное сопротивление не бесконечно, но достаточно велико. Это свойство используется в схемотехнике.
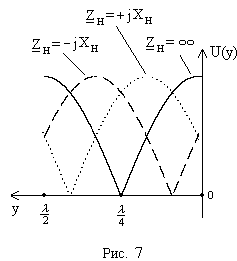 7.3. При нагрузке линии на реактивное сопротивление
7.3. При нагрузке линии на реактивное сопротивление 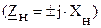 образуются стоячие волны, как и в режимах холостого хода и короткого замыкания. Коэффициент отражения
образуются стоячие волны, как и в режимах холостого хода и короткого замыкания. Коэффициент отражения 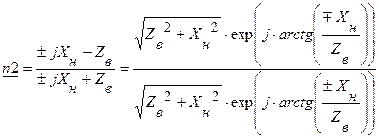 , | n2 |=1. То есть в этом режиме работы длинной линии так же происходит сложение падающей и отражённой волн с равными амплитудами.
, | n2 |=1. То есть в этом режиме работы длинной линии так же происходит сложение падающей и отражённой волн с равными амплитудами.
Реактивный элемент, подключаемый к линии в качестве нагрузки, можно заменить эквивалентным отрезком линии, входное сопротивление которого равно сопротивлению реактивного элемента. Емкостной элемент можно заменить разомкнутым отрезком линии длиной 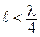 , а индуктивный элемент – короткозамкнутым отрезком длиной
, а индуктивный элемент – короткозамкнутым отрезком длиной 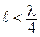 .
.
Если нагрузка индуктивная, узлы и пучности сдвигаются влево, в сторону генератора, и вправо, в сторону нагрузки, если она емкостная (рис. 7).
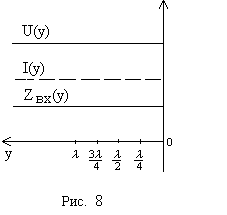 7.4. Если линия нагружена на резистивное сопротивление, равное волновому
7.4. Если линия нагружена на резистивное сопротивление, равное волновому 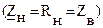 , то нагрузка является согласованной. В этом случае комплексные действующие значения напряжения и тока на выходных зажимах линии связаны соотношением:
, то нагрузка является согласованной. В этом случае комплексные действующие значения напряжения и тока на выходных зажимах линии связаны соотношением: 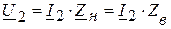 .
.
Напряжение и ток совпадают по фазе, так как в линии без потерь Zв принимает действительное (не комплексное) значение. Коэффициент отражения n2 =0, и в линии существует только падающая волна с неизменной амплитудой (рисунок 8).
Если начальную фазу напряжения 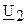 принять равной нулю (
принять равной нулю (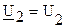 ,
, 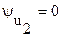 ), то
), то
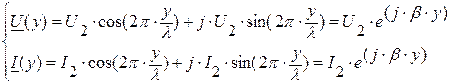 , (7.16)
, (7.16)
тогда мгновенные значения напряжения и тока:
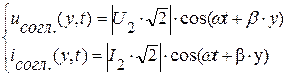 . (7.17)
. (7.17)
В линии без потерь при согласованной нагрузке образуется бегущая волна, амплитуда которой не зависит от расстояния, а фаза – зависит.
Входное сопротивление согласованной линии 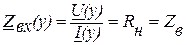 резистивное, равно волновому сопротивлению и не зависит от длины линии.
резистивное, равно волновому сопротивлению и не зависит от длины линии.
7.5. При подключении несогласованной резистивной нагрузки 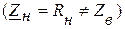 действующие значения напряжения и тока на выходных зажимах линии связаны соотношением:
действующие значения напряжения и тока на выходных зажимах линии связаны соотношением:  , тогда
, тогда
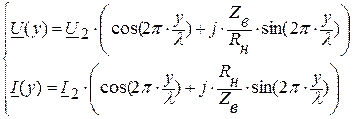
Введём параметр: 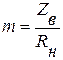 . Коэффициент отражения | n2 |<1. В линии одновременно присутствуют как бегущие, так и стоячие волны. Это можно показать на примере выражения:
. Коэффициент отражения | n2 |<1. В линии одновременно присутствуют как бегущие, так и стоячие волны. Это можно показать на примере выражения:
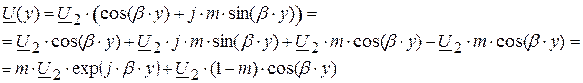
В получившемся выражении первое слагаемое представляет собой бегущую волну (амплитуда не зависит от расстояния; фаза - зависит), а второе слагаемое представляет собой стоячую волну (амплитуда зависит от расстояния по закону cos(βy); фаза - не зависит).
Следовательно, в линии без потерь при резистивной несогласованной нагрузке существует режим смешанных волн.
Распределение действующего значение напряжения вдоль линии описывается выражением:
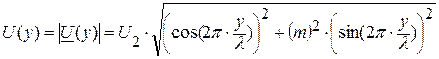 . (7.18)
. (7.18)
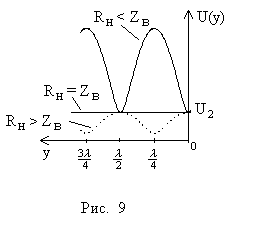
Графики распределения действующих значений напряжения вдоль линии при различных соотношениях между Rн и Zв приведены на рисунке 9.
Чем больше отличие между значениями сопротивления нагрузки Rн и волновым сопротивлением Zв, тем больше отличие между максимальным и минимальным значениями напряжения Umax и Umin. Для количественной оценки этого отличия, то есть степени рассогласования линии с нагрузкой, служит коэффициент бегущей волны:
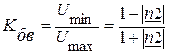 (7.19)
(7.19)
В ряде случаев используют понятие коэффициента стоячей волны: 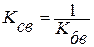 .
.
 2015-03-22
2015-03-22 16269
16269
