Краткая теория. Уравнением в полных дифференциалах называется дифференциальное уравнение

Уравнением в полных дифференциалах называется дифференциальное уравнение

P (x,y)dx + Q(x,y)dy = 0, (12.26)

левая часть которого есть полный дифференциал некоторой функции:

P (x,y)dx + Q (x,y)dy = du(x,y). (12.27)

Уравнение (12.26) с учетом (12.27) можно записать так:

du(x,y) = 0, (12.28)

поэтому его общий интеграл имеет вид

u(x,y) = C. (12.29)

Функция u(x,y) может быть найдена из системы уравнений:

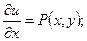
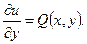(12.30)

Равенство

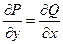
является необходимым и достаточным условием того, что левая часть уравнения (12.26) есть полный дифференциал некоторой функции.

1. Проинтегрировать уравнение

y³ - 2xy)dx + (3xy² - x²)dy = 0.

Это уравнение вида (12.26), для которого

P(x,y) = y³-2xy, Q(x,y) = 3xy²-x².

Находя соответствующие частные производные, получим:

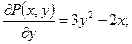
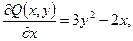
откуда

Следовательно, левая часть уравнения является полным дифференциалом некоторой функции u(x,y):

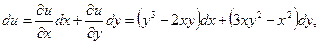
т.е.

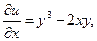
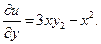(A)

Интегрируем по х первое из уравнений (A), считая у постоянным, при этом вместо постоянной интегрирования надо поставить φ (y) - неизвестную функцию от у:

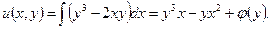
Дифференцируя функцию u(x,y) по у, получим

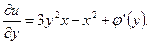
Но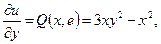

поэтому

3xy² - x² + φ'(y) = 3xy² - x²,

откуда

φ'(y) = 0 и φ(y) = C₁.

Таким образом, u(x,y) = y³x - yx² + C₁.

С другой стороны, по формуле (12.29)

u(x,y) = C₂,

поэтому общий интеграл имеет вид

y³x - x²y = C,

где C = C₂ - C₁.

2. Проинтегрировать уравнение x(x + 2y)dx + (x² - y²)dy = 0.

В данном случае

P(x,y)=x(x+2y), Q(x,y)=x²-y²,

откуда

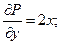
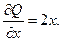
Условие (12.30) выполнено, поэтому данное уравнение является уравнением в полных дифференциалах. Следовательно,

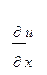= x ² + 2 xy, 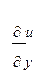= x ² - y ².

Из первого равенства получаем

u (x,y) = 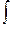(x ²+2 xy) dx или u (x,y) = 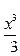+ x²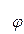y + (y).

Дифференцируя по y функцию u (x,y), находим

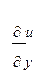= x² + 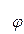' (y).

Так как 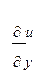= x² - y², то x² + 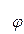' (y) = x² - y²,

откуда 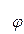' (у) = -y² и 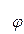(y) = - 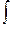y ² dy = - 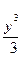+ C ₁.

Подставляя найденное выражение для 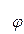(y)в формулу для u (x,y), получим u(x,y) = 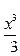+ x²y - 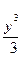+ C ₁ = C ₂ или 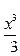+ x²y - 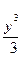= C₃.

Таким образом, общий интеграл можно записать в виде

x ³ + 3 x²y - y³ = C, где C = 3 C₃.

Найти общие интегралы дифференциальных уравнений, предварительно преобразовав их левые части:

12.35.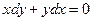

12.37.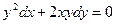

12.36.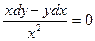

12.38.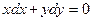

Показать, что данные уравнения являются уравнениями в полных дифференциалах, и найти их общие интегралы:

12.39.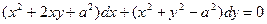

12.40.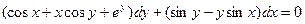

12.41.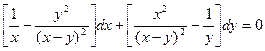

12.7. Задачи, приводящие к дифференциальным уравнениям.