Линейным дифференциальным уравнением первого порядка называется уравнение первой степени относительно у и у', т.е. уравнение вида
φ1(x)y' + φ2(x)y + φ3(x) = 0 (φ1(x) ≠ 0) (12.15)
или
y'+p(x)y = q(x). (12.16)
Решение линейного уравнения ищется в виде
y = u(x)v(x). (12.17)
Подстановка выражений для у и у' в уравнение (12.16) приводит его к виду
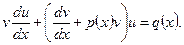 (12.18)
(12.18)
В качестве v выбирают одну из функций, удовлетворяющих уравнению
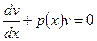 (12.19)
(12.19)
тогда функция u определяется из уравнения
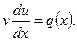 (12.20)
(12.20)
Если функция q(x) ≡ 0, то уравнение (12.16) принимает вид
y' + p(x)y = 0 (12.21)
и называется линейным однородным, его общее решение выражается формулой
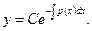 (12.22)
(12.22)
Для решения неоднородного линейного уравнения (12.16) можно применять метод вариации произвольной постоянной. Этот метод состоит в том, что сначала находят общее решение уравнения (12.21), т.е. соотношение (12.22).
Далее, полагая в этом соотношении величину С функцией от х, ищут решение неоднородного уравнения (12.16) в виде (12.22).Для этого подставляют в уравнение (12.16) y и у', определяемые из формулы (12.22), и из полученного дифференциального уравнения находят функцию С(x). Общее решение уравнения (12.16) получается в виде
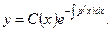 (12.23)
(12.23)
Уравнением Бернулли называется уравнение вида
y' +p(x)y = q(x)yα, (12.24)
где α - действительное число. В случае  α = 0, α = 1 уравнение (12.24) является линейным. Во всех других случаях оно сводится к линейному с помощью подстановки
α = 0, α = 1 уравнение (12.24) является линейным. Во всех других случаях оно сводится к линейному с помощью подстановки
u = y1 – α.. (12.25)
1. Найти общее решение линейного дифференциального уравнения
y' + y - kx = 0.
Данное уравнение является уравнением вида (12.16), где p(x) = 1, q(x) = kx.
Положим y = uv, тогда y' = u'v + uv'. Подставляя эти выражения в исходное уравнение, получим
u'v + uv' + uv – kx = 0 или (v' + v) + u'v – kx = 0. (A)
В качестве v выберем одну из функций, удовлетворяющих уравнению
v' + v = 0 или 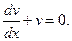 (B)
(B)
Интегрируя это уравнение, получим
ln v = -x, v = e -x.
Уравнение (A) c учетом (B) перепишем так:
u'v - kx = 0 или 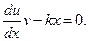
Подставляя сюда значение v = e-x, получим
du - kxexdx = 0.
Интегрируя полученное уравнение, находим
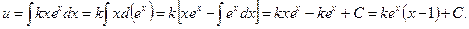
Подставив выражения для u, v в формулу y = u v:
y = uv = e-x[kex (x - 1) + C] = k(x - 1) + Ce-x.
Следовательно, общее решение данного дифференциального уравнения таково:
y = k (x - 1) + Ce-x.
2. Найти общее решение линейного уравнения
xy' – y = x3.
Положим y = uv, тогда y' = u'v + uv'. Уравнение перепишем в виде
x(u'v + uv') – uv = x3 или u(xv' - v) + xu'v = x3. (A)
Выберем v так, чтобы выражение в скобках обратилось в нуль, тогда
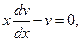
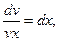 lnv = lnx, v = x.
lnv = lnx, v = x.
Уравнение (A) при v = x запишем так: x2du = x3dx, du = x dx, откуда
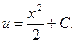
Следовательно, 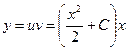 общее решение.
общее решение.
3. Проинтегрировать линейное уравнение
y' + y = x+2.
Пусть y = uv, тогда y' = u'v + uv'.
подставляя выражение для y и y' в уравнение, получим
u'v + uv' + uv = x+2, u(v' + v) = x + 2 - u'v. (A)
Потребуем, чтобы v' + v = 0, тогда
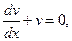
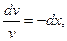 ln v = -x, v = e-x
ln v = -x, v = e-x
Если v' + v = 0, то уравнение (A) принимает вид x+2 - u'v = 0.
Подставляя сюда значение v, перепишем уравнение в виде
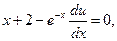
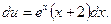
Интегрируя последнее уравнение, получим
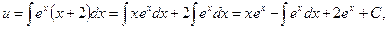
u = xex + ex + C.
Следовательно, у = uv = e-x[C+ex(x+1)].
Таким образом, общее решение дается формулой
у = Ce-x + x+1.
Найти общие решения линейных дифференциальных уравнений первого порядка:
12.25. 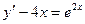
12.27. 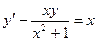
12.29. 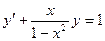
12.31. 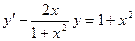
12.26. 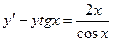
12.28. 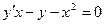
12.30. 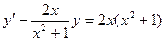
12.32. 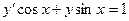
Проинтегрировать уравнения Бернулли:
12.33. 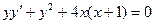
12.34. 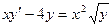
 2015-03-22
2015-03-22 2277
2277
