Краткая теория. Многие научные и технические задачи приводят к интегрированию дифференциальных уравнений

Многие научные и технические задачи приводят к интегрированию дифференциальных уравнений. В таких задачах требуется найти зависимость между переменными величинами некоторого физического, химического или другого процесса, найти уравнение кривой или поверхности и т.п.

При решении этих задач необходимо:

1. Составить дифференциальное уравнение из условия задачи.

2. Определить его тип и выбрать соответствующий метод решения.

3. Проинтегрировать полученное дифференциальное уравнение и получить

его общее решение.

4. Найти частное решение, удовлетворяющее данным начальным условиям.

5. Вычислить по мере необходимости значения вспомогательных параметров

(коэффициент пропорциональности и др.), используя дополнительные

условия задачи.

6. Найти общий закон рассматриваемого процесса и, если это требуется,

численные значения искомых величин.

Приступая к составлению дифференциального уравнения, нужно выбрать независимую переменную и искомую функцию, выразить приращение функции, соответствующее заданному приращению аргумента, через величины, о которых идет речь в условии задачи. Составив отношение приращения функции к приращению аргумента и переходя к пределу, получим дифференциальное уравнение.

При составлении дифференциального уравнения часто бывает целесообразным применить метод дифференциалов, заключающийся в том, что приближенное соотношение между бесконечно малыми приращениями искомых величин, верное с точностью до бесконечно малых высшего порядка, заменяется соответствующим соотношением между их дифференциалами.

Иногда дифференциальное уравнение можно составить более простым путем, воспользовавшись геометрическим или механическим смыслом производной.

Кроме того, при составлении дифференциального уравнения, в зависимости от условия задачи, используются соответствующие законы физики, механики, химии и других наук.

1. Точка движется по прямой линии с постоянным ускорением.

Найти закон движения точки.

В качестве независимой переменной выберем время, тогда пройденный путь и скорость точки будут функциями времени.

Обозначим путь, пройденный за время t, через s, скорость точки - через v и ускорение через w.

По условию w = a, где a - постоянная величина. Пусть в начальный

момент времени заданы значение скорости v₀ и значение пути s₀, т.е.

v = v₀, s = s₀ при t = 0, где v₀ и s₀ - некоторые постоянные.

Так как ускорение точки при прямолинейном движении равно производной скорости по времени, то по условию задачи можно составить следующее дифференциальное уравнение первого порядка с разделяющимися переменными:

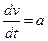или dv=adt.

Интегрируя последнее уравнение, получаем v = at + C₁. Значение постоянной C₁ определим по начальным условиям: v = v₀ при t = 0.

Подставляя эти значения v и t в выражение v, найдем:

v₀ = a 0 + C₁, C₁ = v₀.

Следовательно, скорость движения точки выразится формулой

v = a t + v₀.

Подставляя в эту формулу выражение для скорости v через производную от пути по времени

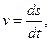
получим новое дифференциальное уравнение первого порядка с разделяющимися переменными

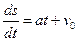или ds=(at+v₀)dt.

Интегрируя это уравнение, найдем общее решение данной задачи

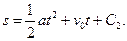
Так как s = s₀ при t = 0, то C₂ = s₀, следовательно,

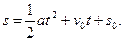
В частности, полагая в выражениях для v и s a = g, v₀ = 0, s₀ = h,

s = h получим закон движения при свободном падении в пустоте:

v = gt,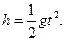

2. Движение фондов. Обозначим через К величину фондов в натуральном или стоимостном выражении. Фонды – это станки, помещения и т.п. Все это ломается, изнашивается, стареет и т.д. Про этот процесс говорят, что фонды выбывают. Скорость выбытия фондов выражают через коэффициент выбытия. Так, если за 10 лет фонды полностью обновляются, то коэффициент выбытия равен 1/10. Обозначим коэффициент выбытия через 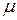. Итак, выбытие ведет к уменьшению фондов за год на величину 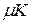, а за время 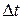на величину 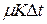(считаем, что выбытие фондов происходит равномерно). С другой стороны, инвестиции – вложения денег – ведут к увеличению фондов. Предположим, что инвестиции в размере I за год дадут увеличение фондов на величину 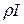(можно было бы считать, что 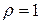, но часть инвестиций идет на зарплату проектировщикам, строителям, т.е. не на прямое увеличение фондов), тогда за время 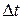инвестиции при их равномерном вложении дадут увеличение фондов на величину .

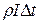Рассмотрим произвольный момент времени t и его приращение 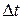. Тогда имеем 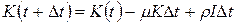и, устремляя 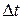к нулю, получим дифференциальное уравнение 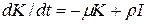. Подчеркнем, что I – константа.

3. Демографическая задача. Обозначим население страны в момент t через 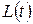. Представляется естественным предположение, что увеличение населения за время 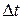пропорционально численности населения L и 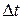, тогда 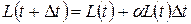. Устремляя 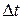к нулю, получим дифференциальное уравнение 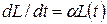. Можно догадаться, что его общее решение есть 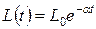, где 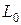– численность населения в момент 0 (начало наблюдения). Такой закон роста населения называется экспоненциальным. Ясно, однако, что он не может продолжаться сколько-нибудь длительное время – включатся противодействующие механизмы: снижение жизненного уровня, меры по ограничению рождаемости и т.п., и рост населения затормозится.

Составить дифференциальные уравнения из условий следующих задач и решить их:

12.42. Найти кривую, проходящую через точку М(1;3) и для которой отрезок касательной между точкой касания с осью Оx делится пополам в точке пересечения с осью Оy.

12.43. Найти такую кривую, проходящую через точку М(0;3), чтобы угловой коэффициент касательной в любой ее точке равнялся ординате этой точки, уменьшенной на две единицы.

12.44. Через сосуд емкостью 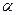литров, наполненный водным раствором соли, непрерывно протекает жидкость, причем в единицу времени вливается b литров чистой воды и вытекает такое же количество раствора. Найти закон, по которому изменяется содержание соли в сосуде в зависимости от времени протекания жидкости через сосуд.

12.45. Лодка замедляет свое движение под действием сопротивления воды, которое пропорционально скорости лодки. Начальная скорость лодки 1,5 м/сек., скорость ее через 4 сек 1 м/сек. Когда скорость уменьшится до 0,01 м/сек? Какой путь может пройти лодка до остановки?

12.46. Тело охладилось за 20 мин от 100° до 60°. Температура окружающего воздуха поддерживается равной 20°. Когда тело остынет до 30°?

12.47. В баке находится 100 литров раствора, содержащего 10 кг соли. В бак непрерывно подается вода со скоростью 5 литров в минуту. Поступающая в бак вода перемешивается с имеющимся раствором, и смесь вытекает с той же скоростью. Сколько соли останется в баке через 1 час?

12.48. Найти кривую, все нормали которой проходят через постоянную точку.

12.49. Вода вытекает через отверстие в дне цилиндрического сосуда. По какому закону понижается уровень воды с течением времени, если известно, что скорость 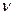, с которой жидкость вытекает из отверстия, зависит от высоты 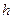столба жидкости следующим образом: .

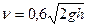12.50. Судно водоизмещением 12000 тонн движется прямолинейно со скоростью 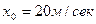. Сопротивление воды пропорционально квадрату скорости судна и равно 36 т при скорости 1 м/сек. Какое расстояние пройдет судно после остановки двигателя, прежде чем скорость станет равной 5 м/сек? В какое время судно пройдет это расстояние?