P(x,y)dx + Q(x,y)dy = 0 (12.11)
называется однородным, если коэффициенты P(x,y) и Q(x,y) являются однородными функциями одного и того же измерения n, т.е. функциями, для которых при любом k выполняются тождества
P(kx,ky) = kn P(x,y), Q(kx,ky) = kn Q(x,y). (12.12)
Уравнение (11) можно привести к виду
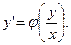 (12.13)
(12.13)
С помощью подстановки y = ux, (12.14)
где u - новая неизвестная функция, однородное уравнение преобразуется в уравнение с разделяющимися переменными.
1. Проинтегрировать однородное дифференциальное уравнение
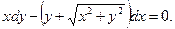
Коэффициенты при dy и dx соответственно равны:
Q(x,y) = x; 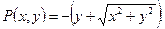
Функции P(x,y) и Q(x,y) являются однородными функциями первой степени.
Действительно, Q(kx, ky) = kx = kQ(x,y);
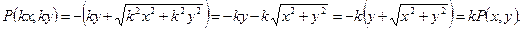
Таким образом, тождества (12.12) выполняются.
Положим y = ux, тогда dy = udx + xdu. Подставим эти выражения в исходное уравнение:
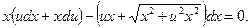
Раскрывая скобки, приводя подобные члены и сокращая на х, получим уравнение с разделяющимися переменными
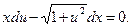
Разделяя переменные и интегрируя, находим
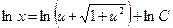
откуда 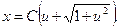 .
.
Подставляя сюда выражение 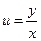 (полученное из равенства у = ux), находим
(полученное из равенства у = ux), находим 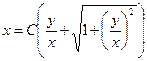 или
или 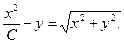
Возведя в квадрат обе части уравнения и сокращая на x2 , получим общий интеграл
x2 - 2Cy = C 2.
2. Найти общий интеграл однородного уравнения
(x2-y2)dy - 2xу dx = 0.
В данном случае имеем:
Q(x,y) = x2-y2; P(x,y) = - 2xy.
Эти функции являются однородными функциями второй степени.
В самом деле:
Q(kx,ky) = (kx)2 - (ky)2 = k2(x2-y2) ≡ k2Q(x,y);
P(kx,ky) = -2(kx)(ky) = k2(-2xy) ≡ k2P(x,y).
Полагая y = ux, находим dy = x du + u dx.
Подставляя выражения для y и dy в исходное уравнение и сокращая на x2 ≠ 0, получаем уравнение с разделяющимися переменными:
(1-u2)(x du+u dx)-2u dx = 0 или 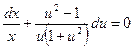 (u ≠ 0).
(u ≠ 0).
Принимая во внимание, что
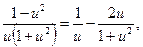
и интегрируя полученное уравнение, находим ln|x| = ln|u| - ln|1+u2| + ln|C|, откуда
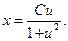
Подставляя сюда выражение для u, определяемое из равенства y = ux, получим общий интеграл
x2+y2=Cy,
представляющий семейство окружностей с центрами на оси Oy и проходящий через начало координат.
Замечание. При u = 0 получаем решение y = 0. Это решение является частным. В самом деле, общий интеграл x2 + y2 = Cy можно переписать в виде C1(x2+y2) = y, где 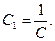 При C1 = 0 получаем y = 0.
При C1 = 0 получаем y = 0.
Проинтегрировать однородные дифференциальные уравнения:
12.13. 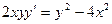
12.15. 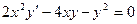
12.17. 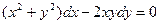
12.19. 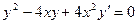
12.21 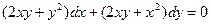
12.14. 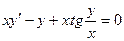
12.16. 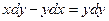
12.18. 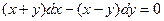
12.20. 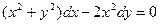
12.22. 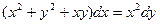
Проинтегрировать уравнения, приводящие к однородным:
12.23. 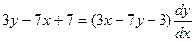 12.24.
12.24. 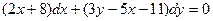
 2015-03-22
2015-03-22 2785
2785
