1. Ряд называется абсолютно сходящимся, если сходится как сам, так и ряд, составленный из абсолютных величин его членов.
Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.
2. Достаточный признак сходимости знакопеременного ряда.. Если ряд, составленный из абсолютных величин членов данного ряда, сходится, то сходится и данный ряд.
3. Ряд называется знакочередующимся, если его члены попеременно то положительны, то отрицательны: 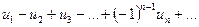 , где
, где 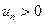
4. Признак Лейбница. Если члены знакочередующегося ряда убывают по абсолютной величине, т.е. 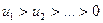 , и предел модуля его общего члена равен нулю, т.е.
, и предел модуля его общего члена равен нулю, т.е.
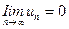 , (13.5)
, (13.5)
то ряд сходится, а его сумма не превосходит первого члена: S 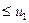
5. Пусть знакочередующийся ряд 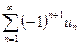 удовлетворяет условиям признака Лейбница и пусть Sn — его n-я частичная сумма. Тогда ряд сходится, и погрешность rn = S - Sn при приближенном вычислении его суммы S по абсолютной величине не превосходит модуля первого отброшенного члена:
удовлетворяет условиям признака Лейбница и пусть Sn — его n-я частичная сумма. Тогда ряд сходится, и погрешность rn = S - Sn при приближенном вычислении его суммы S по абсолютной величине не превосходит модуля первого отброшенного члена:
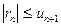 , (13.6)
, (13.6)
а для его суммы S при любом п выполняется неравенство:
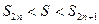 (13.7)
(13.7)
13.68. Выяснить, какие из данных рядов являются сходящимися, а какие — расходящимися. Для сходящихся рядов определить, сходятся они абсолютно или условно.
а) 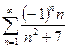 ; б)
; б) 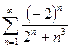 ; в)
; в) 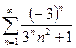
Решение:
а) В данном случае 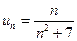 . При
. При 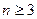 члены данного знакочередующегося ряда убывают по абсолютной величине,
члены данного знакочередующегося ряда убывают по абсолютной величине, 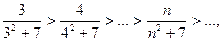 и
и 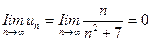 Отбрасывание конечного числа членов ряда не влияет на его сходимость, поэтому по признаку Лейбница (п. 4) ряд сходится.
Отбрасывание конечного числа членов ряда не влияет на его сходимость, поэтому по признаку Лейбница (п. 4) ряд сходится.
Определим тип сходимости ряда. Для этого исследуем сходимость ряда, составленного из модулей членов данного ряда. Его члены равны, 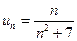 Применим предельный признак сравнения (§13.2, п. 2). Рассуждая так же, как и при решении примера 13.14, в качестве эталонного ряда возьмем гармонический ряд,
Применим предельный признак сравнения (§13.2, п. 2). Рассуждая так же, как и при решении примера 13.14, в качестве эталонного ряда возьмем гармонический ряд,
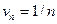 .
. 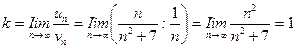 ,
,
т.е. предел k конечен и отличен от нуля, и исследуемый ряд ведет себя так же, как и эталонный ряд. Из расходимости эталонного ряда следует расходимость исследуемого ряда.
Таким образом, сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится, т.е. ряд сходится условно.
б) Члены этого ряда имеют разные знаки, поэтому, следуя п. 5, § 13.1, найдем
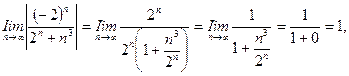
ибо 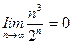 (это можно проверить трехкратным применением правила Лопиталя). Предел модуля общего члена ряда отличен от нуля, поэтому (§ 13.1, п. 5) ряд расходится.
(это можно проверить трехкратным применением правила Лопиталя). Предел модуля общего члена ряда отличен от нуля, поэтому (§ 13.1, п. 5) ряд расходится.
в) Члены данного ряда убывают по абсолютной величине и
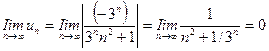 , ибо при
, ибо при 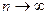
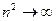 , а
, а 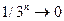 .
.
Следовательно, по признаку Лейбница ряд сходится.
Исследуем сходимость ряда, составленного из модулей членов даннoгo ряда. Его члены имеют вид 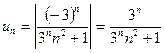 . Применим предельный признак сравнения.
. Применим предельный признак сравнения.
В качестве эталонного ряда возьмем сходящийся ряд с членами 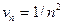 . Имеем
. Имеем
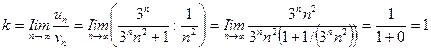
предел k конечен и отличен от нуля, следовательно, исследуемый ряд ведет себя так же, как и эталонный ряд, т.е. сходится. Таким образом, сходится как сам ряд, так и ряд, составленный из абсолютных величин его членов, т.е. ряд сходится абсолютно.
13.69. Найти сумму ряда 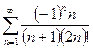 с точностью до 0,0001.
с точностью до 0,0001.
Решение. У данного ряда 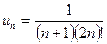 , его члены удовлетворяют условиям признака Лейбница, поэтому ряд сходится. Для того чтобы определить количество членов, подлежащих суммированию для вычисления суммы ряда с заданной точностью, будем выписывать члены ряда до тех пор, пока не найдем член, по модулю меньший, чем 0,0001 = 1/10 000:
, его члены удовлетворяют условиям признака Лейбница, поэтому ряд сходится. Для того чтобы определить количество членов, подлежащих суммированию для вычисления суммы ряда с заданной точностью, будем выписывать члены ряда до тех пор, пока не найдем член, по модулю меньший, чем 0,0001 = 1/10 000:
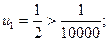
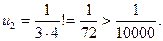
Таким образом, для достижения требуемой точности достаточно вычислить 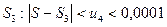 (п. 5), т.е. достаточно взять три первых члена ряда:
(п. 5), т.е. достаточно взять три первых члена ряда:
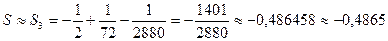
Результат должен быть получен с точностью до 0,0001, поэтому окончательный ответ не может содержать более 4 цифр после запятой. При последнем округлении была допущена дополнительная ошибка, не превосходящая 0,00005. Итоговая ошибка при вычислении суммы ряда не больше 0,00005 + 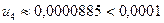
13.70. Для суммы S ряда 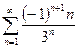 выбрать наиболее точную оценку:
выбрать наиболее точную оценку:
а) 4/81<S<13/243; б) 1/9<S<2/9; в) 14/81<S<47/243.
Решение. Данный рад удовлетворяет условиям признака Лейбница, поэтому 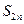 < S < S2n+1. (13.7). Найдем несколько первых частичных сумм по формуле (13.1):
< S < S2n+1. (13.7). Найдем несколько первых частичных сумм по формуле (13.1):
|
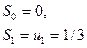 0<S<
0<S< 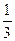 ;
;
|
|
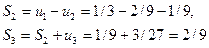
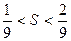
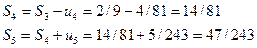
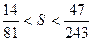
Таким образом, неравенство п. а) для суммы S данного ряда не выполняется, т.е. вообще не является оценкой для S. Неравенства (б) и (в) верны для S, поэтому они являются оценками S, Из них более точной оказалась оценка пункта (в).
Выяснить, какие из данных рядов являются сходящимися, а какие — расходящимися. Для сходящихся рядов определить, сходятся они абсолютно или условно:
13.71. 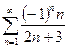 . 13.72.
. 13.72. 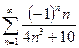 . 13.73.
. 13.73. 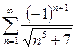 .
.
13.74. 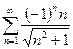 . 13. 75.
. 13. 75. 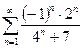 . 13.76..
. 13.76.. 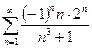 .
.
13.77. 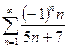 . 13.78.
. 13.78. 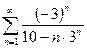 . 13.79.
. 13.79. 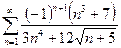 .
.
13.80. 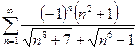 . 13.81.
. 13.81. 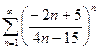 . 13.82.
. 13.82. 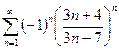 .
.
13.83. 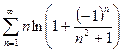 .
.
13.84. 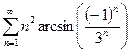 .
.
Определить, сколько членов ряда надо взять, чтобы вычислить его сумму с точностью до 0,0001:
13.85. 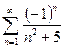 . 13.86.
. 13.86. 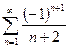 . 13.87.
. 13.87. 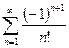 . 13.88.
. 13.88. 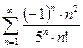 .
.
Найти сумму ряда с точностью до 0,00001. В ответе также указать, сколько членов ряда надо взять, чтобы гарантировать требуемую точность:
13.89. 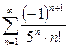 .
.
13.90. 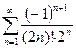 .
.
 2015-03-22
2015-03-22 2798
2798
