1. Числовым рядом называется бесконечная последовательность чисел, соединенных знаком сложения: 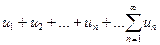 .
.
Числа u1,u2,... un... называются членами ряда, член un — общим или n -м членом ряда, сумма и первых членов ряда 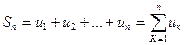 (13.1)
(13.1)
называется n -й частичной суммой ряда.
2. Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, т.е. 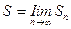 . (13.2)
. (13.2)
Число S называется суммой ряда. Если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся.
3. Отбрасывание иди приписывание к ряду конечного числа членов не влияет на сходимость или расходимость ряда.
4. Если ряд 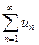 сходится, то предел его общего члена при
сходится, то предел его общего члена при 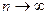 равен нулю:
равен нулю: 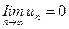 (необходимое условие сходимости ряда).
(необходимое условие сходимости ряда).
5. При нарушении необходимого условия сходимости ряда, если предел общего члена ряда при 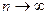 не существует или если он не равен нулю, ряд расходится. Заметим, что если предел общего члена ряда равен нулю, то вывод о сходимости или расходимости ряда можно сделать только после дополнительного исследования.
не существует или если он не равен нулю, ряд расходится. Заметим, что если предел общего члена ряда равен нулю, то вывод о сходимости или расходимости ряда можно сделать только после дополнительного исследования.
Для рядов с членами разных знаков удобнее пользоваться эквивалентными формулировками: если предел модуля общего члена ряда равен нулю, т.е. если 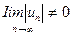 , то ряд расходится, а если предел модуля общего члена ряда равен нулю, т.е. если
, то ряд расходится, а если предел модуля общего члена ряда равен нулю, т.е. если 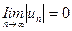 , то вывод о сходимости или расходимости ряда можно сделать только после дополнительного исследования.
, то вывод о сходимости или расходимости ряда можно сделать только после дополнительного исследования.
13.1. Выяснить, является ли ряд 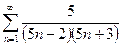 сходящимся.
сходящимся.
В случае положительного ответа найти сумму ряда.
Решение. Для того чтобы ответить на вопрос о сходимости ряда, надо найти предел последовательности частичных сумм 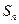 , если он существует (п. 2). Представим
, если он существует (п. 2). Представим
n -й член ряда в виде разности дробей со знаменателями (5 n - 2) и (5 n + 3):
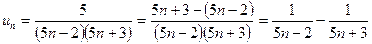
Найдем частичную сумму по формуле (13.1):
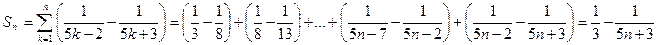
Найдем предел: 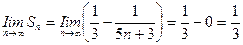
Предел последовательности частичных сумм ряда конечен, он равен 1/3. Это значит, что исследуемый ряд сходится (п. 2), и его сумма равна 1/3.
13.2. Для данных рядов найти  В тех случаях, где этого достаточно для установления сходимости или расходимости ряда, сделать вывод о поведении ряда:
В тех случаях, где этого достаточно для установления сходимости или расходимости ряда, сделать вывод о поведении ряда:
а) 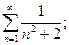 б)
б) 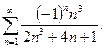
Решение:
а) Общий член ряда имеет вид 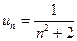 . Найдем его предел:
. Найдем его предел: 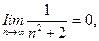
как предел отношения ограниченной функции и бесконечно большой величины. Поскольку предел общего члена ряда равен нулю, вывод о сходимости или расходимости ряда можно сделать только после дополнительного исследования.
б) Общий член ряда имеет вид 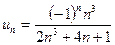 , ряд имеет и положительные, и отрицательные члены, поэтому находим предел модуля общего члена:
, ряд имеет и положительные, и отрицательные члены, поэтому находим предел модуля общего члена:
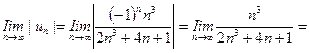
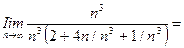
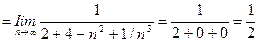 .
.
Поскольку предел модуля общего члена не равен нулю, необходимое условие сходимости ряда не выполняется, и исследуемый ряд расходится.
13.3. Исследовать сходимость ряда 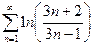 .
.
Решение. Общий член ряда имеет вид 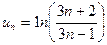 . Найдем предел n -го члена:
. Найдем предел n -го члена:
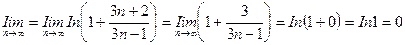 .
.
Это значит, что для ответа на вопрос о сходимости ряда требуется дополнительное исследование. Воспользуемся определением сходимости ряда. Найдем выражение для частичных сумм ряда (13.1):
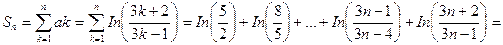
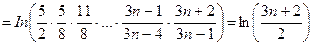 .
.
Здесь мы воспользовались тем, что сумма логарифмов равна логарифму произведения. Далее, 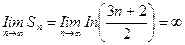 , ибо при
, ибо при 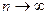 выражение в скобках и логарифм от него стремятся к бесконечности. Таким образом, предел последовательности частичных сумм ряда бесконечен, и поэтому (п. 2) исследуемый ряд расходится.
выражение в скобках и логарифм от него стремятся к бесконечности. Таким образом, предел последовательности частичных сумм ряда бесконечен, и поэтому (п. 2) исследуемый ряд расходится.
Найти частичную сумму ряда Sn. В случае сходимости ряда найти его сумму:
13.4. 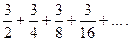
13.5. 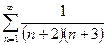 .
.
13.6. 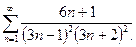
13.7. 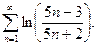
Для данных рядов найти 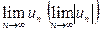 В тех случаях, где этого достаточно для установления сходимости или расходимости ряда, сделать вывод о поведении ряда:
В тех случаях, где этого достаточно для установления сходимости или расходимости ряда, сделать вывод о поведении ряда:
13.8. 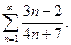
13.9. 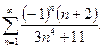
13.10. 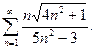
13.11. 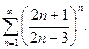
13.12. 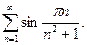
13.13. 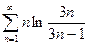 .
.
13.2. Признаки сходимости рядов с положительными членами
 2015-03-22
2015-03-22 1838
1838
