Краткая теория. 1. Если функция f(x) имеет производные любого порядка в окрестности точки х = 0, то для функции f(x) может быть получен ряд Маклорена

1. Если функция f (x) имеет производные любого порядка в окрестности точки
х = 0, то для функции f (x) может быть получен ряд Маклорена:

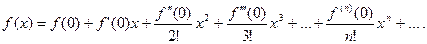(14.4)

Для того, чтобы ряд Маклорена (14.4) сходился к функции f (x), необходимо и достаточно, чтобы при n → ∞, остаток ряда стремился к нулю, т.е.

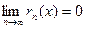(14.5)

для всех значений х из интервала сходимости ряда.

2. Разложение в ряд Маклорена некоторых функций[1]

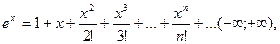(14.6)

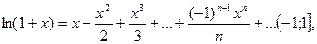(14.7)

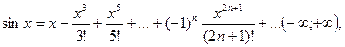(14.8)

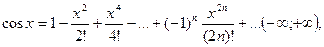(14.9)

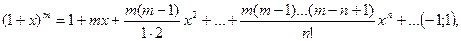(14.10)

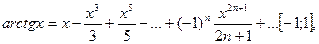(14.11)

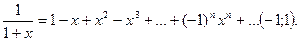(14.12)

3. Ряд Маклорена (при х ₀=0) является частным случаем ряда Тейлора:

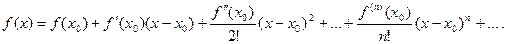(14.13)

Ряд Тейлора тесно связан с формулой Тейлора:

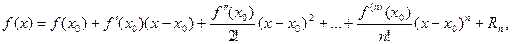(14.14)

где 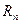- остаточный член формулы Тейлора:

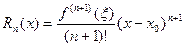(14.15)

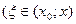или 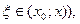записанный в форме Лагранжа.

При выполнении условия (14.5) остаток 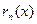ряда Тейлора равен остаточному члену 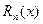формулы Тейлора.

4. Свойства степенных рядов:

а) Если f (x) – сумма степенного ряда, т.е. 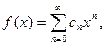то на любом отрезке [ a, b ], целиком принадлежащем интервалу сходимости (- R; R), функция f (x) является непрерывной, а степенной ряд можно почленно интегрировать на этом отрезке:

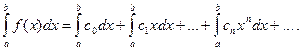(14.16)

б) В интервале сходимости степенной ряд можно почленно дифференцировать:

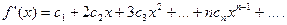(14.17)

При этом ряды (14.16) и (14.17) имеют тот же радиус сходимости R, что и исходный ряд (14.1).

5. Если в некоторой окрестности точки х =0 имеют место разложения

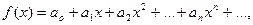(14.18)

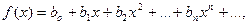(14.19)

то произведение функции f (x) φ (x) разлагается в той же окрестности в степенной ряд

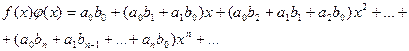(14.20)

(правило перемножения рядов).

В частности, при f (x)= φ (x)

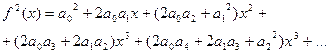(14.21)

(правило возведения ряда в квадрат).

Почленное интегрирование и дифференцирование степенных рядов (свойства (14.16), (14.17)) могут быть использованы при нахождении суммы степенного ряда.

14.22. Найти сумму ряда при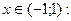

а)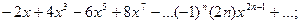

б)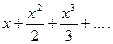

Решение:

а) Можно заметить, что полученное интегрирование данного ряда (на отрезке [0; x ], где 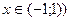приведет к геометрическому ряду (14.22), сумма которого известна:

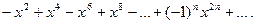(14.22)

Полагая 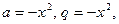найдем сумму ряда (14.22):

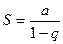или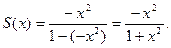

Возвращаясь к исходному ряду, находим его сумму дифференцированием S (x). Итак, сумма данного в условии ряда

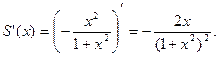
б) Данный ряд может быть приведен почленным дифференцированием в интервале сходимости к геометрическому ряду 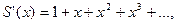сумма которого равна 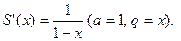Сумму исходного ряда находим интегрированием на отрезке [0;x], где :

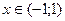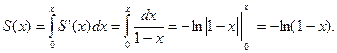
Существует несколько способов разложения функций в степенной ряд. Проиллюстрируем их на конкретных примерах.