1. Степенным рядом называется ряд
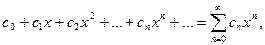 (14.1)
(14.1)
где 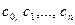 - коэффициенты степенного ряда.
- коэффициенты степенного ряда.
2. Областью сходимости степенного ряда называется совокупность тех значений х, при которых степенной ряд (14.1) сходится.
3. Число R – такое, что при | х |< R ряд (14.1) сходится, а при | х |> R – расходится, называется радиусом сходимости степенного ряда.
Интервал (-R; R) называется интервалом сходимости степенного ряда. При х = -R, x =R ряд может как сходиться, так и расходиться.
4. Радиус сходимости степенного ряда может быть найден по формуле:
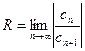 . (14.2)
. (14.2)
Формула (14.2) применима, если, начиная с некоторого номера n, все 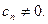
Для степенного ряда вида
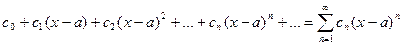 (14.3)
(14.3)
радиус сходимости находится по формуле (14.2), а интервал сходимости из условия | х-а | < R, т.е. имеет вид: (а-R, a+R).
14.1. Найти области сходимости степенных рядов:
а) 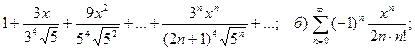
в) 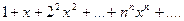
Решение:
а) Найдем радиус сходимости ряда по формуле (14.2):
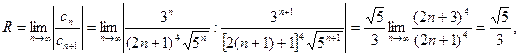
т.е. интервал сходимости ряда 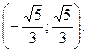
Теперь выясним поведение ряда на концах интервала сходимости. На левом конце при 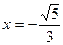 данный степенной ряд принимает вид
данный степенной ряд принимает вид 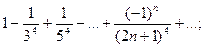 этот ряд сходится по признаку Лейбница. На правом конце при
этот ряд сходится по признаку Лейбница. На правом конце при 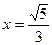 получаем ряд
получаем ряд 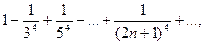 представляющий обобщенный гармонический ряд при
представляющий обобщенный гармонический ряд при
α = 4, у которого все члены с четными номерами равны нулю. Так как α = 4 >1, то этот ряд сходится.
Следует отметить, что сходимость ряда на левом конце интервала сходимости при 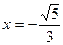 могла быть установлена с помощью достаточного признака сходимости знакопеременного ряда, так как ряд, составленный из абсолютных величин его членов, т.е. ряд
могла быть установлена с помощью достаточного признака сходимости знакопеременного ряда, так как ряд, составленный из абсолютных величин его членов, т.е. ряд 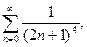 сходится. Итак, область сходимости данного ряда
сходится. Итак, область сходимости данного ряда 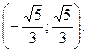
Обращаем внимание на то, что при исследовании сходимости степенного ряда на концах интервала сходимости в ситуации, когда получаемый ряд – с положительными членами, применять признак Даламбера не имеет смысла, так как при этом всегда будем получать 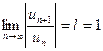 с нерешенным вопросом о сходимости ряда: в этом случае рекомендуется рассматривать другие признаки сходимости (например, признак сравнения, интегральный, необходимый признаки и т.д.)
с нерешенным вопросом о сходимости ряда: в этом случае рекомендуется рассматривать другие признаки сходимости (например, признак сравнения, интегральный, необходимый признаки и т.д.)
б) Найдем радиус сходимости по формуле (14.2):
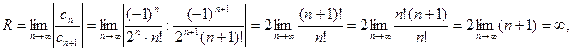
т.е. область сходимости ряда (-∞;+∞).
в) Задачу можно решать аналогично предыдущим. Решение упрощается, если заметить, что при х ≠ 0 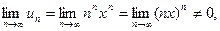 т.е. необходимый признак сходимости не выполняется, и ряд расходится.
т.е. необходимый признак сходимости не выполняется, и ряд расходится.
Итак, область сходимости ряда состоит из одной точки х = 0.
Найти области сходимости степенных рядов:
14.2. 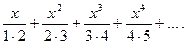
14.3. 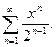
14.4. 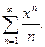
14.5. 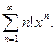
14.6. 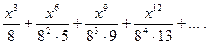
14.7. 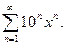
14.8. 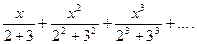
14.9. 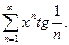
14.10. 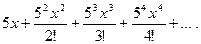
14.11. 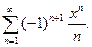
14.12. 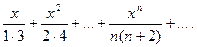
14.13. 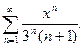
14.14. 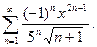
14.15. 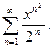
14.16. 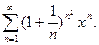
14.17. 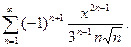
14.18. 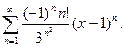
14.19. 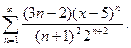
14.20. 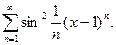
14.21. 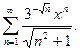
14.2. Ряды Тейлора и Маклорена.Формула Тейлора
 2015-03-22
2015-03-22 872
872








