1. Признак сравнения. Пусть 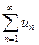 и
и 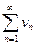 — два ряда с положительными членами, и пусть члены первого ряда не превосходят членов второго, т.е.
— два ряда с положительными членами, и пусть члены первого ряда не превосходят членов второго, т.е. 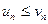 при любом n. Тогда:
при любом n. Тогда:
а) если сходится ряд 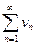 , то сходится и ряд
, то сходится и ряд 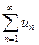
б) если расходится ряд 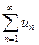 то расходится и ряд
то расходится и ряд 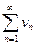 .
.
2. Предельный признак сравнения. Если 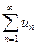 и
и 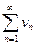 — ряды с положительными членами и существует конечный предел отношения их общих членов
— ряды с положительными членами и существует конечный предел отношения их общих членов
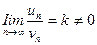 , (13.3)
, (13.3)
то ряды либо одновременно сходятся, либо одновременно расходятся.
3. Ряд, с которым сравнивается исследуемый ряд, будем называть эталонным. Наиболее часто, в качестве эталонного используют либо гармонический ряд 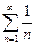
(он расходится), либо обобщенный гармонический ряд 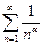 (при а > 1 он сходится, а при
(при а > 1 он сходится, а при 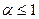 — расходится), либо геометрический ряд
— расходится), либо геометрический ряд 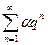 (при |q|<1 он сходится, при |q|
(при |q|<1 он сходится, при |q| 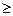 1— расходится).
1— расходится).
4. Признак Даламбера. Пусть для ряда 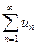 с положительными членами существует предел отношения (n +1)-го члена к n -му:
с положительными членами существует предел отношения (n +1)-го члена к n -му: 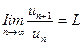 (13.4)
(13.4)
Тогда при L< 1 ряд сходится, при L > 1 и при L = 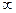 ряд расходится, а при L = 1 для ответа на вопрос о сходимости ряда требуется дополнительное исследование.
ряд расходится, а при L = 1 для ответа на вопрос о сходимости ряда требуется дополнительное исследование.
5. Интегральный признак сходимости. Пусть дан положительный ряд 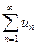 и пусть функция f(х) такая, что f(1) = u1, f(2) = u2…, f(n) = un,..., непрерывна и не возрастает при х
и пусть функция f(х) такая, что f(1) = u1, f(2) = u2…, f(n) = un,..., непрерывна и не возрастает при х 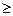 1. Тогда для сходимости ряда
1. Тогда для сходимости ряда 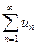 необходимо и достаточно, чтобы сходился несобственный интеграл
необходимо и достаточно, чтобы сходился несобственный интеграл 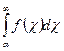 при некотором а
при некотором а 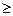 1.
1.
13.14. С помощью признаков сравнения исследуйте данные ряды на сходимость:
а) 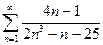 ; б)
; б) 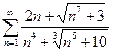 ; в)
; в) 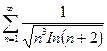 ;
;
г) 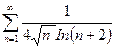 ; д)
; д) 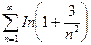 ; е)
; е) 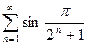 .
.
Решение:
а) Несколько членов данного ряда не являются положительными. Если отбросить конечное число членов этого ряда, он станет знакоположительным. Отбрасывание конечного числа членов ряда не влияет на сходимость или расходимость ряда (§ 13.1, п. 3), поэтому к этому ряду можно применить предельный признак сравнения. Если общий член ряда представляет собой отношение двух многочленов, то при подборе эталонного обобщенного гармонического ряда значение а выбирают равными разности наибольших показателей степеней знаменателя и числителя. Наибольший показатель степени знаменателя равен 3, числителя — 1, поэтому
а = 3 – 1 = 2, и в качестве эталонного ряда возьмем обобщенный гармонический ряд с членами vn=1-n2.
По формуле (13.3):
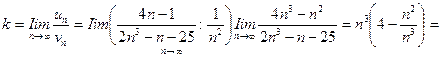
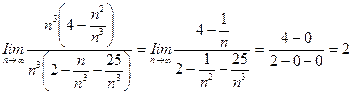 .
.
Поскольку предел k конечен и отличен от нуля, условие (13.3) выполнено. На основании предельного признака сравнения заключаем, что исследуемый ряд 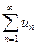 и эталонный ряд
и эталонный ряд 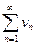 ведут себя одинаково. Эталонный ряд сходится (обобщенный гармонический ряд, а = 2, п. 3), поэтому исследуемый ряд тоже сходится.
ведут себя одинаково. Эталонный ряд сходится (обобщенный гармонический ряд, а = 2, п. 3), поэтому исследуемый ряд тоже сходится.
Замечание 1. Вычисление предела k необходимо для проверки правильности подбора эталонного ряда. Если получим, что k = 0 или k = 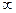 , то для применения предельного признака сравнения следует взять другой эталонный ряд.
, то для применения предельного признака сравнения следует взять другой эталонный ряд.
б) Применим предельный признак сравнения. Подберем подходящий эталонный ряд. Рассмотрим поведение числителя и знаменателя общего члена ряда при больших n: 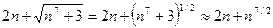 ,
, 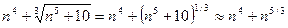 . Поскольку при больших n величина n 7/2 много больше, чем n, а величина n4 много больше, чем n5/3, то числителю условно припишем показатель степени 7/2, а знаменателю — 4. Возьмем а = 4-7/2 = 1/2, и в качестве эталонного ряда рассмотрим обобщенный гармонический ряд с членами
. Поскольку при больших n величина n 7/2 много больше, чем n, а величина n4 много больше, чем n5/3, то числителю условно припишем показатель степени 7/2, а знаменателю — 4. Возьмем а = 4-7/2 = 1/2, и в качестве эталонного ряда рассмотрим обобщенный гармонический ряд с членами 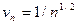 . Найдем
. Найдем
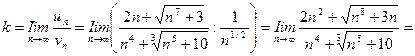
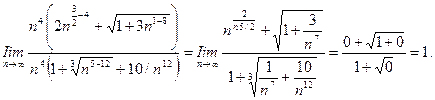
Предел k конечен и отличен от нуля, условие (13.3) предельного признака сравнения выполнено (п. 2). Эталонный ряд расходится (обобщенный гармонический ряд, а = 1/2, п. 3), поэтому исследуемый ряд тоже расходится.
в) Попытки применить предельный признак сравнения с эталонным рядом вида 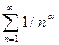 не приводят к успеху: при разных а предел k равен или нулю, или бесконечности. Применим первый признак сравнения (п. 1). Подберем эталонный ряд. При увеличении n функция n растет гораздо быстрее, чем функция In (n + 2), поэтому возьмем
не приводят к успеху: при разных а предел k равен или нулю, или бесконечности. Применим первый признак сравнения (п. 1). Подберем эталонный ряд. При увеличении n функция n растет гораздо быстрее, чем функция In (n + 2), поэтому возьмем 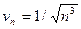 . При
. При 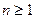 выполняется цепочка неравенств:
выполняется цепочка неравенств: 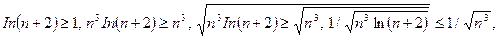 т.е.
т.е. 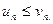
Эталонный ряд 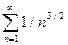 является обобщенным гармоническим рядом, у которого
является обобщенным гармоническим рядом, у которого
а = 3 / 2 > 1, поэтому он сходится (п. 3). Члены исследуемого ряда не превосходят членов сходящегося ряда, значит, исследуемый ряд сходится (п. 1).
г) Как и в пункте в), попытки применить предельный признак сравнения с эталонным рядом вида 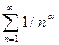 не приводят к успеху: при разных а предел k равен или нулю, или бесконечности. Применим признак сравнения (п. 1). Подберем эталонный ряд. При увеличении n при всех а > 0 функция n
не приводят к успеху: при разных а предел k равен или нулю, или бесконечности. Применим признак сравнения (п. 1). Подберем эталонный ряд. При увеличении n при всех а > 0 функция n 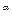 растет гораздо быстрее, чем функция
растет гораздо быстрее, чем функция 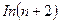 . Возьмем
. Возьмем 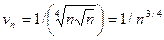 .
.
При достаточно больших n выполняется неравенство 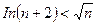 , откуда
, откуда 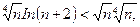
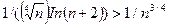 т.е.
т.е. 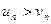 . Эталонный ряд
. Эталонный ряд 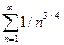 является обобщенным гармоническим рядом, а = 3/4 < 1, поэтому он расходится (п. 3). Члены исследуемого ряда больше членов расходящегося ряда, значит, исследуемый ряд расходится (п. 1).
является обобщенным гармоническим рядом, а = 3/4 < 1, поэтому он расходится (п. 3). Члены исследуемого ряда больше членов расходящегося ряда, значит, исследуемый ряд расходится (п. 1).
Замечание2. В примере г) при подборе эталонного ряда нельзя просто отбросить In (n + 2). Если взять 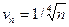 , то, как и в примере в), можно показать, что
, то, как и в примере в), можно показать, что 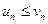 . Однако ряд pacxoдится (а = 1/4 < 1), и члены исследуемого ряда не больше членов расходящегося ряда, а в этом случае предельный признак сравнения не дает ответа на вопрос о сходимости или расходимости ряда
. Однако ряд pacxoдится (а = 1/4 < 1), и члены исследуемого ряда не больше членов расходящегося ряда, а в этом случае предельный признак сравнения не дает ответа на вопрос о сходимости или расходимости ряда 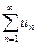 .
.
д) Применим предельный признак сходимости. При 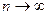 бесконечно малая величина
бесконечно малая величина 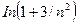 эквивалентна 3/n2, и в качестве эталонного ряда возьмем ряд с членами
эквивалентна 3/n2, и в качестве эталонного ряда возьмем ряд с членами 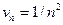 . По формуле (13.3) найдем
. По формуле (13.3) найдем
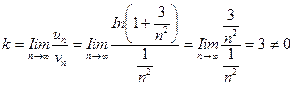 .
.
Эталонный ряд сходится, и с ним вместе сходится исследуемый ряд.
е) Решение аналогично п. д). При 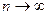 бесконечно малая величина
бесконечно малая величина 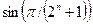 эквивалентна
эквивалентна 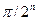 , и в качестве эталонного ряда возьмем ряд с членами
, и в качестве эталонного ряда возьмем ряд с членами 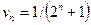 — (см. начало гл. 6, п. 11). По формуле (13.3) найдем k =
— (см. начало гл. 6, п. 11). По формуле (13.3) найдем k = 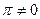 . Эталонный ряд сходится, и с ним вместе сходится исследуемый ряд.
. Эталонный ряд сходится, и с ним вместе сходится исследуемый ряд.
Замечание3. В примерах а) — д) признак Даламбера не дает ответа на вопрос о сходимости рядов — во всех этих случаях
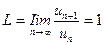 . В примере е) L = 1/2, применение признака Даламбера возможно.
. В примере е) L = 1/2, применение признака Даламбера возможно.
13.15. Исследовать сходимость рядов с помощью признака Даламбера:
а) 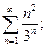 б)
б) 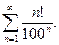
Решение:
а) Для того чтобы вычислить 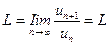 , преобразуем
, преобразуем 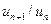 :
:
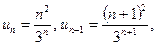 и
и 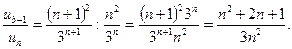
Далее,
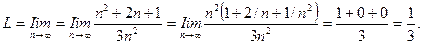
Поскольку L = 1/3 < 1, то по признаку Даламбера (п. 4) исследуемый ряд сходится.
б) Имеем 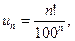
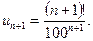 Напомним, что по определению факториала
Напомним, что по определению факториала
n!= 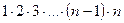 . Найдем L по формуле (13.4):
. Найдем L по формуле (13.4):
 .
.
Поскольку L= 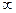 , то по признаку Даламбера (п. 4) исследуемый ряд расходится.
, то по признаку Даламбера (п. 4) исследуемый ряд расходится.
13.16. Исследовать сходимость ряда 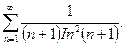
Решение. Применим интегральный признак сходимости. Рассмотрим
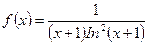 . Эта функция удовлетворяет всем условиям интегрального признака. По определению несобственного интеграла (11.22)
. Эта функция удовлетворяет всем условиям интегрального признака. По определению несобственного интеграла (11.22)
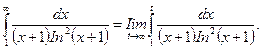
Найдем
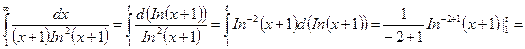
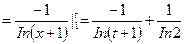
(при вычислении определенного интеграла мы воспользовались тем, что 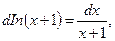 и применили формулу Ньютона—Лейбница (11.11). Далее,
и применили формулу Ньютона—Лейбница (11.11). Далее,

Поскольку предел конечен, несобственный интеграл сходится, и по интегральному признаку сходимости (п. 5) исследуемый ряд тоже сходится.
Замечание. При попытке использовать признак Даламбера для исследования сходимости данного ряда получим, что L = 1, т.е. необходимо дополнительное исследование. При попытке найти эталонный ряд вида 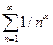 и применить предельный признак сравнения получим, что k - 0 при
и применить предельный признак сравнения получим, что k - 0 при 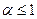 или k =
или k = 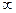 при а > 1, т.е. применение предельного признака сравнения с эталонным обобщенным гармоническим рядом невозможно. Также невозможно исследовать сходимость этого ряда с помощью эталонных рядов вида
при а > 1, т.е. применение предельного признака сравнения с эталонным обобщенным гармоническим рядом невозможно. Также невозможно исследовать сходимость этого ряда с помощью эталонных рядов вида 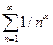 и первого признака сравнения (п. 1), поскольку члены исследуемого ряда при
и первого признака сравнения (п. 1), поскольку члены исследуемого ряда при 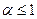 меньше членов расходящихся рядов, а при а > 1 они больше членов сходящихся рядов. В этих ситуациях признак сравнения дает ответа на вопрос о сходимости ряда.
меньше членов расходящихся рядов, а при а > 1 они больше членов сходящихся рядов. В этих ситуациях признак сравнения дает ответа на вопрос о сходимости ряда.
Исследовать сходимость рядов с помощью предельного признака сравнения. В качестве эталонного ряда рассмотреть ряд с общим членом 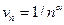 . В ответе указать подходящее значение
. В ответе указать подходящее значение 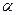 .
.
13.17. 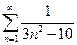 . 13.18.
. 13.18.  . 13.19.
. 13.19. 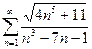 .
.
13.20. 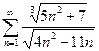 . 13.21.
. 13.21. 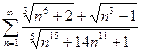 . 13.22.
. 13.22. 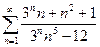 .
.
13.23. 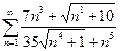 . 13.24.
. 13.24. 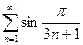 . 13.25.
. 13.25. 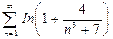 .
.
13.26. 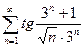 . 13.27.
. 13.27. 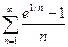 . 13.28.
. 13.28. 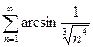 .
.
Исследовать данные ряды на сходимость, применив признаки сравнения:
13.29. 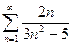 . 13.30.
. 13.30. 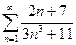 . 13.31.
. 13.31. 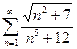 .
.
13.32. 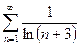 . 13.33
. 13.33 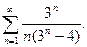 13.34
13.34 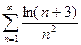 .
.
13.35. 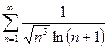 13.36.
13.36. 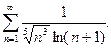 13.37.
13.37. 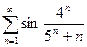 .
.
13.38. 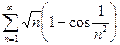 .
.
Выяснить, можно ли исследовать сходимость данных радов с помощью признака Даламбера. В случае положительного ответа сделать вывод о поведении ряда. В ответе также указать полученное значение l (см. (13.4)):
13.39. 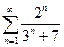 . 13.40.
. 13.40. 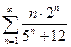 . 13.41.
. 13.41. 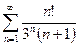 .
.
13.42. 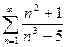 . 13.43.
. 13.43. 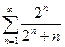 . 13.44.
. 13.44. 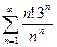 .
.
13.45. 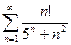 . 13.46.
. 13.46. 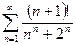 13.47.
13.47. 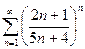 .
.
13.48. 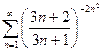 . 13.49.
. 13.49. 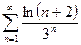 . 13.50.
. 13.50. 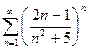 .
.
13.51. 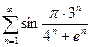 . 13.52.
. 13.52. 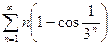 .
.
С помощью интегрального признака исследовать сходимость рядов:
13.53. 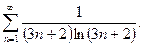 13.54.
13.54. 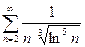 13.55.
13.55. 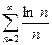
Исследовать сходимость рядов:
13.56. 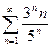 . 13.57.
. 13.57. 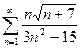 . 13.58.
. 13.58. 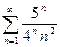 .
.
13.59. 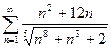 . 13.60.
. 13.60. 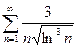 . 13.61.
. 13.61. 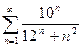 .
.
13.62. 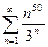 . 13.63.
. 13.63. 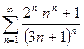 . 13.64.
. 13.64. 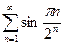 .
.
13.65. 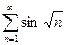 . 13.66.
. 13.66. 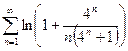 . 13.67.
. 13.67. 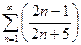 .
.
13.3. Сходимость рядов с членами произвольного знака
 2015-03-22
2015-03-22 2171
2171
