14.27. Разложить в ряд по степеням х функцию y = arcsin x.
Решение. Среди готовых разложений (14.6)-(14.12) ряда для данной функции нет. В то же время производная этой функции 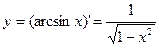 может быть разложена в степенной ряд с помощью биноминального ряда (14.10) (см. пример 14.24, б):
может быть разложена в степенной ряд с помощью биноминального ряда (14.10) (см. пример 14.24, б):
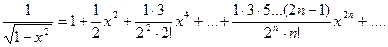
Учитывая, что 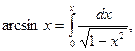 искомый ряд найдем почленным интегрированием данного ряда на отрезке [0; x ], принадлежащем интервалу сходимости ряда (-1;1):
искомый ряд найдем почленным интегрированием данного ряда на отрезке [0; x ], принадлежащем интервалу сходимости ряда (-1;1):
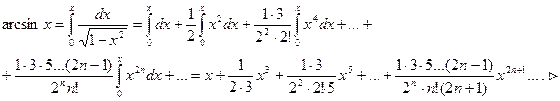
14.28. Разложить в ряд по степеням х функцию 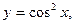 применяя различные способы.
применяя различные способы.
Решение:
Первый способ. Применим метод непосредственного разложения по формуле (14.4).
Вначале найдем производные до n -го порядка и вычислим их значения при х = 0:
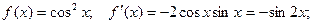
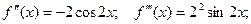
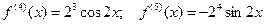 и т.д.
и т.д.
Теперь по формуле (14.4) запишем ряд:
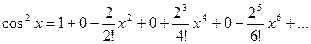
или
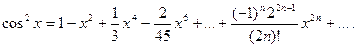
Область сходимости ряда, как нетрудно убедиться, есть (- ∞;+ ∞).
Второй способ. Учитывая, что 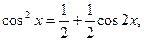 используем готовое разложение в ряд (14.9) функции cos x (в котором вместо х берем 2 х), умножаем обе части полученного равенства на
используем готовое разложение в ряд (14.9) функции cos x (в котором вместо х берем 2 х), умножаем обе части полученного равенства на 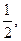 а затем прибавляем к ним
а затем прибавляем к ним 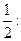
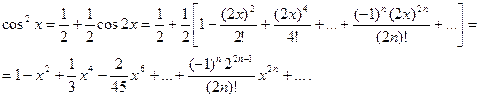
Третий способ. Для функции f (x)=cos x, имеющей разложение (14.9), т.е.
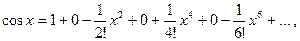
применим правило (14.19) возведения в квадрат степенного ряда:
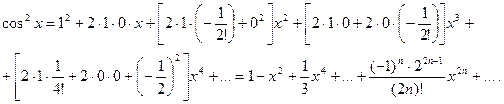
Четвертый способ. Относительно легко можно разложить в ряд производную функции 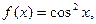 т.е.
т.е. 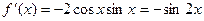 (берем члены ряда (14.8) с противоположными знаками, а вместо х берем 2 х):
(берем члены ряда (14.8) с противоположными знаками, а вместо х берем 2 х):
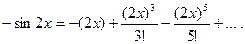
Для получения искомого разложения почленно интегрируем полученный ряд на отрезке [0; x ], принадлежащем интервалу сходимости (- ∞;+ ∞), т.е. при любом х:
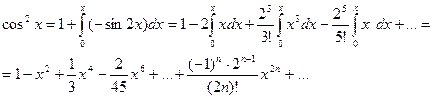
(к полученному почленным интегрированием ряду добавили 1, так как 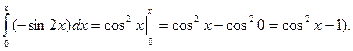
Разложить в степенной ряд по степеням х функции:
14.29. 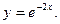 14.30.
14.30. 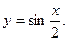 14.31.
14.31. 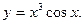
14.32. 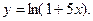 14.33.
14.33. 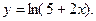 14.34.
14.34. 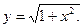
14.35. 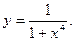 14.36.
14.36. 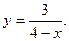 14.37.
14.37. 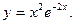
14.38. 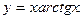 . 14.39.
. 14.39. 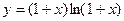 . 14.40.
. 14.40. 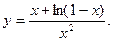
14.41. 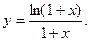 14.42.
14.42. 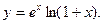 14.43.
14.43. 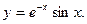
14.44. 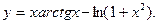 14.45.
14.45. 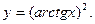 14.46.
14.46. 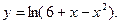
14.47. 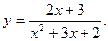
Разлагая подынтегральную функцию в ряд по степеням х и интегрируя его почленно, найти разложения в ряд функций:
14.48. 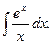 14.49.
14.49. 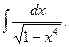 14.50.
14.50. 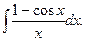
Разложить в степенной ряд функции:
14.51. 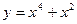 по степеням (х -1). 14.52.
по степеням (х -1). 14.52. 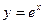 по степеням (х -2).
по степеням (х -2).
14.53. 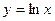 по степеням (х -1). 14.54.
по степеням (х -1). 14.54. 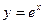 по степеням (х +2).
по степеням (х +2).
Применяя почленное интегрирование или дифференцирование рядов, найти их суммы:
14.55. 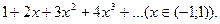 14.56.
14.56. 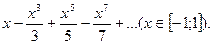
14.57. 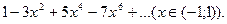
14.3. Применение рядов в приближенных вычислениях
Степенные ряды могут быть использованы для приближенного вычисления значений различных функций, определенных интегралов (в том числе «неберущихся»), нахождения пределов и т.п.
14.58. Вычислить приближенно с точностью до 0,0001:
а) 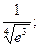 б)
б) 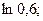 в)
в) 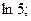 г)
г) 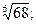 д)
д) 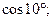 е)
е) 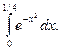
Решение:
а) Для вычисления 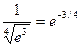 запишем ряд (14.6) при х = -3/4, принадлежащем области сходимости (-∞;+∞):
запишем ряд (14.6) при х = -3/4, принадлежащем области сходимости (-∞;+∞):
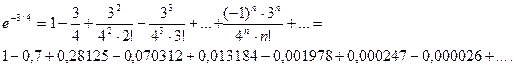
Взяв первые семь членов разложения, на основании следствия из теоремы Лейбница (гл. 13.3, п. 5) для сходящегося знакочередующегося ряда мы допустим погрешность 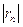 , не превышающую первого отброшенного члена (по абсолютной величине), т.е.
, не превышающую первого отброшенного члена (по абсолютной величине), т.е.
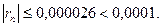
Итак, складывая первые семь членов, получим
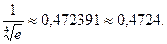
Более точно оценить погрешность вычисления 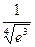 можно, используя формулу Тейлора (14.14). Взяв в качестве величины
можно, используя формулу Тейлора (14.14). Взяв в качестве величины 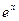 первые (n +1) членов ряда (вместе с нулевым), мы допускаем погрешность, определяемую остаточным членом
первые (n +1) членов ряда (вместе с нулевым), мы допускаем погрешность, определяемую остаточным членом 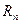 (14.15) при
(14.15) при 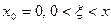 или
или 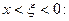
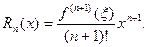
Для функции 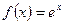
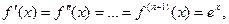 т.е.
т.е. 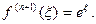 Следовательно, при х = -3/4
Следовательно, при х = -3/4
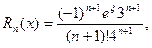 где
где 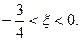
При n = 6, т.е. просуммировав вместе с нулевым 7 членов ряда, мы получим 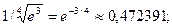 при этом остаточный член
при этом остаточный член 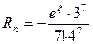 заключен в границах от минимального
заключен в границах от минимального 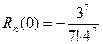 до максимального
до максимального 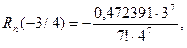 т.е.
т.е.
–0,000026< Rn <–0,000013. Следовательно, точное значение 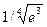 находится в пределах 0,472365<
находится в пределах 0,472365< 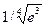 <0,472378. Неизменны 4 десятичных знака, следовательно, с точностью до δ =0,0001
<0,472378. Неизменны 4 десятичных знака, следовательно, с точностью до δ =0,0001 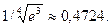
(Легко показать, что суммирование менее, чем семь членов ряда (n <6), не обеспечивает данной в условии точности ответа.)
б) Для вычисления ln0,6 запишем ряд (14.7) при х = -0,4, входящем в область сходимости ряда (-1;1]:
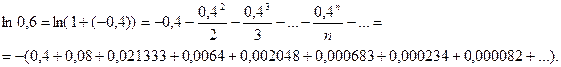
Если в качестве ln0,6 взять первые восемь членов, мы допустим погрешность
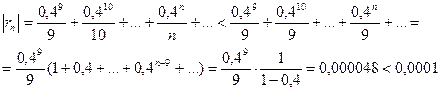
(мы учли, что сумма сходящегося геометрического ряда в скобках равна 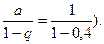
Итак, складывая первые восемь членов, получим:
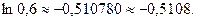
Заметим, что при суммировании только семи членов погрешность 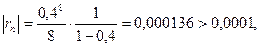 т.е. не удовлетворяет заданной в условии точности до 0,0001.
т.е. не удовлетворяет заданной в условии точности до 0,0001.
Замечание. Оценка погрешности вычисления ln0,6 с помощью остаточного члена формулы Тейлора оказывается в данном случае менее эффективной. Действительно, для функции f (x)=ln(1+ x)
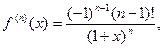 тогда по формуле (14.15) остаточный член
тогда по формуле (14.15) остаточный член
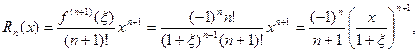
где 0 < ξ < х или х < ξ < 0.
При n = 8, x = -0,4 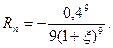 Следовательно,
Следовательно, 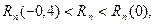 или
или 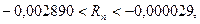 а значит,
а значит, 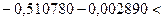
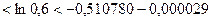 , т.е.
, т.е. 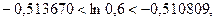 что гарантирует точность вычисления лишь до 0,01 (а точнее, до 0,003).
что гарантирует точность вычисления лишь до 0,01 (а точнее, до 0,003).
в) Вычислить ln3 = ln(1+2) с помощью ряда (14.7) для функции y = ln(1+ x) не представляется возможным, так как х = 2 не входит в область сходимости ряда (-1;1].
Воспользуемся рядом, приведенным в гл. 14.2:
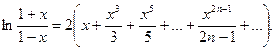 (14.23)
(14.23)
Этот ряд позволяет вычислять логарифмы любых чисел, так как при изменении х в интервале сходимости ряда (-1;1) дробь 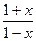 меняется в интервале (0;+∞).
меняется в интервале (0;+∞).
Пусть 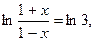 тогда
тогда 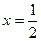 и
и
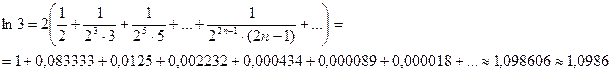
(суммируем семь членов ряда – обоснование аналогично п. б).
Ряд (14.23) по сравнению с рядом (14.7) быстрее сходится, и потому удобнее для вычисления логарифмов. Так, если для вычисления ln0,6 с точностью до 0,0001 потребовалось суммировать восемь членов ряда (14.7) – см. п. б), то с помощью ряда (14.23) та же точность достигается при сложении лишь трех членов.
г) Представим 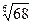 в виде
в виде 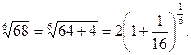 Так как после проведенного преобразования
Так как после проведенного преобразования 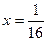 входит в область сходимости (-1;1) биноминального ряда (14.10), то при
входит в область сходимости (-1;1) биноминального ряда (14.10), то при 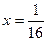 ,
, 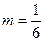 получим, учитывая (14.10):
получим, учитывая (14.10):
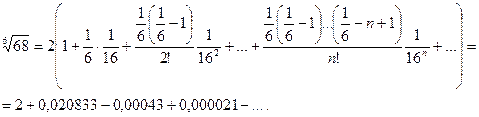
(Для обеспечения данной в условии точности расчета достаточно взять три члена, так как по следствию из признака Лейбница для сходящегося знакочередующегося ряда погрешность 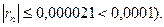 Итак,
Итак, 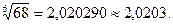
д) Для вычисления 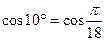 запишем ряд (14.9) при
запишем ряд (14.9) при 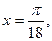 принадлежащем области сходимости (-∞;+∞):
принадлежащем области сходимости (-∞;+∞):
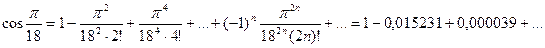
(необходимо взять два члена, так как при этом погрешность 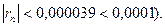
Итак, 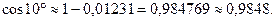
е) «Точное» интегрирование здесь невозможно, так как интеграл «неберущийся». Заменив х на (- х 2) в разложении (14.6), получим
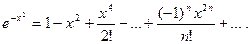
Почленно интегрируя ряд на отрезке 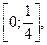 принадлежащем интервалу сходимости ряда (-∞;+∞), получим
принадлежащем интервалу сходимости ряда (-∞;+∞), получим
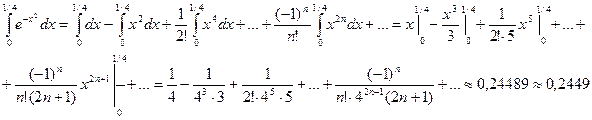 (оценка погрешности производится также, как в примерах а), г) и д)).
(оценка погрешности производится также, как в примерах а), г) и д)).
14.59. Найти пределы:
а) 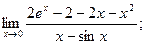 б)
б) 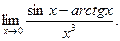
Решение. Нахождение указанных пределов требует неоднократного применения правила Лопиталя (с учетом первого замечательного предела, либо использования эквивалентных бесконечно малых). Вместе с тем эти пределы относительно легко могут быть вычислены, если использовать разложение входящих в них функций в степенные ряды.
а) Заменим 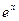 и
и 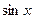 их разложениями (14.6), (14.8) в степенные ряды. Получим
их разложениями (14.6), (14.8) в степенные ряды. Получим
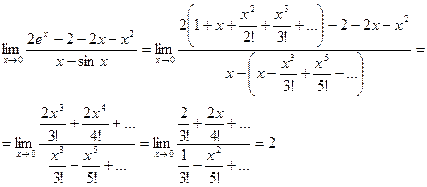
б) Заменяя 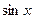 и
и 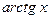 их разложениями (14.8), (14.11) в степенные ряды, найдем
их разложениями (14.8), (14.11) в степенные ряды, найдем
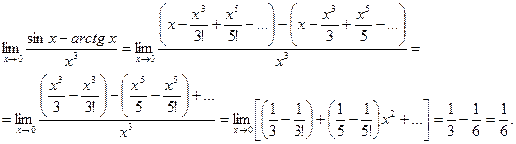
Вычислить приближенно с точностью δ:
14.60. 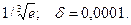
14.61. 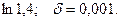
14.62. 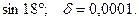
14.63. 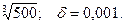
14.64. 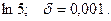
14.65. 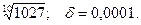
14.66. 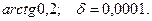
14.67. 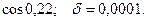
14.68. 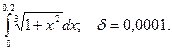
14.69. 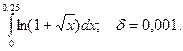
14.70. 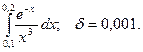
14.71. 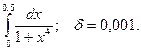
14.72. 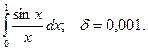
14.73. 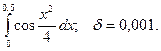
14.74. 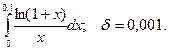
14.75. 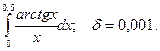
Вычислить приближенное значение интегралов, взяв три члена разложения подынтегральной функции в ряд; указать погрешность:
14.76. 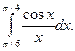 14.77.
14.77. 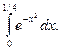
Найти пределы:
14.78. 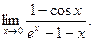 14.79.
14.79. 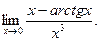
14.80. 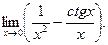 14.81.
14.81. 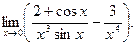
14.82. Прибыль от реализации продукции промышленного предприятия растет в зависимости от роста удельного веса р высококачественных изделий в общем объеме выпуска продукции по формуле 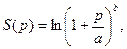 где а >1, 0≤ р ≤0,2. Аппроксимировать функцию
где а >1, 0≤ р ≤0,2. Аппроксимировать функцию 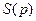 линейной и оценить получаемую при этом погрешность.
линейной и оценить получаемую при этом погрешность.
Указание. Воспользоваться разложением функции ln(1+ x) в ряд Маклорена. При оценке погрешности считать р максимально возможным.
 2015-03-22
2015-03-22 3093
3093








