2015-03-22
646
14.24. Разложить в ряд по степеням х функции:
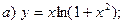
Решение:
а) Воспользуемся готовым разложением (14.7) функции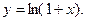 
Заменяя в нем 
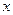на 
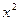, получим
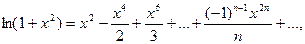
следовательно
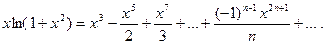
Область сходимости ряда [-1;1] находим из условия -1< х 2≤1.
б) Воспользуемся биноминальным рядом (14.10), представляющим разложение в ряд функции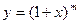 
. Заменив в нем 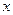на 
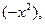получим при 
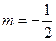разложение функции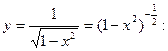 
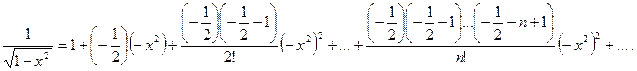
Умножая обе части разложения на 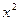, получим
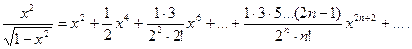
Область сходимости ряда (-1;1) находим из условия -1<- х 2<1.
14.25. Разложить в ряд по степеням (х -1) функцию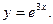 
Решение. Представим функцию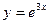 
в виде: 
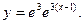Это позволяет использовать готовое разложение (14.6) функции 
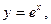в котором х заменяем на
3 (х – 1):
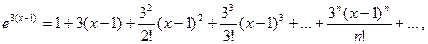
откуда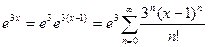 
(записываем ряд в сокращенном виде).
Область сходимости ряда (-∞;+∞) находим из условия -∞<3(х -1)<∞.
