1. Частными производными функции 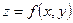 по
по 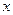 и по
и по 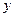 называются пределы вида:
называются пределы вида:
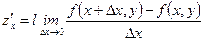 ;
; 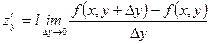 . (15.1)
. (15.1)
2. Дифференциалом функции 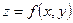 называется сумма произведений частных производных этой функции на приращения независимых переменных
называется сумма произведений частных производных этой функции на приращения независимых переменных
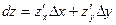 (15.2)
(15.2)
или 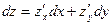 , (15.3)
, (15.3)
учитывая, что 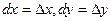 . (15.4)
. (15.4)
3. Производной 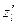 по направлению
по направлению 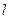 функции
функции 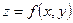 называется предел
называется предел
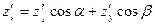 . (15.5)
. (15.5)
Производная по направлению может быть выражена через частные производные по формуле 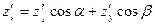 , (15.6)
, (15.6)
где единичный вектор 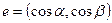 задает направление
задает направление 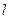 (с углами
(с углами 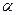 и
и 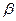 , образуемыми с осями координат).
, образуемыми с осями координат).
4. Градиентом функции 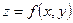 называется вектор
называется вектор 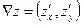 . (15.7)
. (15.7)
Градиент функции в точке 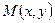 , отличный от нуля, перпендикулярен линии уровня, проходящего через эту точку.
, отличный от нуля, перпендикулярен линии уровня, проходящего через эту точку.
15.27. Найти частные производные функции 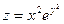 .
.
Решение. При дифференцировании по 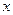 считаем постоянной величину
считаем постоянной величину 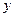 .Таким образом,
.Таким образом, 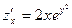 . При дифференцировании по
. При дифференцировании по 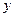 считаем постоянной величину
считаем постоянной величину 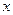 , следовательно,
, следовательно, 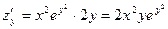 .
.
15.28. Найти частные производные второго порядка функции двух переменных 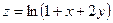 .
.
Решение. Частные производные 1 – го порядка имеют вид:
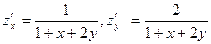 .
.
Считая их новыми функциями двух переменных, найдем их частные производные. Получаем:
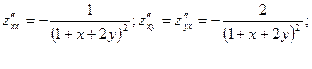
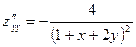 .
.
15.29. Найти длину вектора 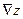 градиента функции
градиента функции 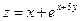 в точке (0;0).
в точке (0;0).
Решение. Компонентами вектора 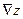 (15.7) являются частные производные функции, т.е.
(15.7) являются частные производные функции, т.е. 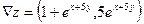 . В точке (0;0) получаем
. В точке (0;0) получаем 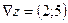 . Соответственно длина вектора
. Соответственно длина вектора 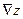 равна
равна 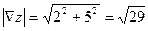 .
.
15.30. Найти производную функции 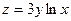 в точке (2;0) по направлению, параллельному биссектрисе первого координатного угла.
в точке (2;0) по направлению, параллельному биссектрисе первого координатного угла.
Решение. Прямая, проходящая через точку (2,0) параллельно биссектрисе первого координатного угла, задается уравнением 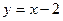 (см. (4.7)). Ее углы с осями координат (как и у биссектрисы) равны
(см. (4.7)). Ее углы с осями координат (как и у биссектрисы) равны 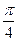 . Следовательно. По формуле (15.6):
. Следовательно. По формуле (15.6):
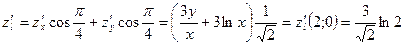 .
.
Найти частные производные функций:
15.31. 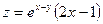 . . | 15.32. 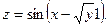 | 15.33. 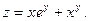 |
15.34. 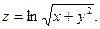 | 15.35. 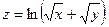 | 15.36. 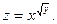 |
15.37. 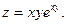 | 15.38. 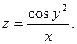 | 15.39. 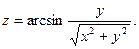 |
Найти полные дифференциалы функций:
15.41. 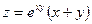 . 15.42.
. 15.42. 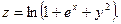 15.43.
15.43. 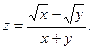
15.44. 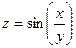 . 15.45.
. 15.45. 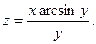 15.46.
15.46. 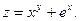
Найти производные функций по заданным направлениям l:
15.47. 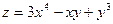 ; l составляет с осью Ох угол
; l составляет с осью Ох угол 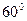 .
.
15.48. 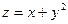 ; l – биссектриса 1-го координатного угла.
; l – биссектриса 1-го координатного угла.
15.49. Вычислить производную функции 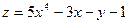 в точке М(2;1)
в точке М(2;1)
по направлению l – прямой МN, где N (5,5).
15.50. Вычислить производную функции 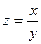 в точке М(1;1) по направлению l – перпендикуляра к прямой y = 2х – 1.
в точке М(1;1) по направлению l – перпендикуляра к прямой y = 2х – 1.
Найти градиент функции z = f(x,y) и его модуль для функций в указанных точках М:
15.51. 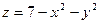 ; М(1;2 ). 15.52.
; М(1;2 ). 15.52. 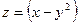 ; М(0;3).
; М(0;3).
15.53. 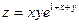 ; М(0;-1 ). 15. 54.
; М(0;-1 ). 15. 54. 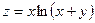 ; М(-1;2 ).
; М(-1;2 ).
15.55. 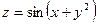 ; М
; М 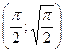 .
.
15.3. Экстремум функции нескольких переменных. Условный экстремум
 2015-03-22
2015-03-22 1860
1860
