1. Если каждому набору 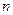 переменных
переменных 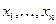 из некоторого множества
из некоторого множества 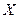 соответствует одно вполне определенное значение переменной
соответствует одно вполне определенное значение переменной 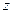 , то говорят, что задана функция нескольких переменных
, то говорят, что задана функция нескольких переменных 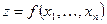 .
.
Множество 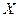 называется областью определения функции.
называется областью определения функции.
2. График функции двух переменных 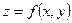 есть множество точек трехмерного пространства (
есть множество точек трехмерного пространства (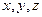 ) и представляет собой, как правило, некоторую поверхность.
) и представляет собой, как правило, некоторую поверхность.
Линией уровня функции двух переменных 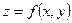 называется множество точек на плоскости, таких, что во всех этих точках значение функции одно и то же и равно
называется множество точек на плоскости, таких, что во всех этих точках значение функции одно и то же и равно 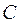 . Число
. Число 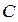 в этом случае называется уровнем.
в этом случае называется уровнем.
3. Число  называется пределом функции
называется пределом функции 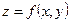 при,, если для любого числа
при,, если для любого числа 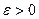 найдется
найдется 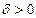 , зависящее от
, зависящее от 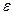 , такое, что для всех точек
, такое, что для всех точек 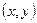 , отстоящих от точки
, отстоящих от точки 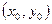 не более, чем на
не более, чем на 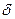 , выполняется неравенство
, выполняется неравенство 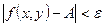 .
.
15.1. Найти область определения функции 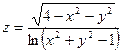 .
.
Решение. Область определения представляет собой решение системы неравенств:
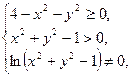
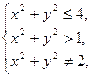

Множество значений х, у, удовлетворяющих (*), представляет собой внутренность круга с центром (0; 0) и радиусом, равным 2. Решения (**) – внешность круга радиуса 1 с центром (0; 0). Условие (***) означает, что в область определения не входит окружность с центром в начале координат и радиусом, равным 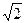 . Таким образом, область определения представляет собой два кольца (см. рис. 15.1).
. Таким образом, область определения представляет собой два кольца (см. рис. 15.1).
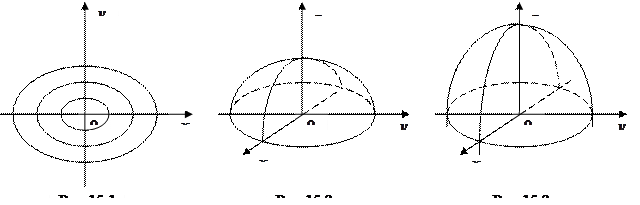
15.2. Построить графики функций:
а) 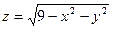 ; б)
; б) 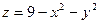 .
.
Решение:
а) Так как 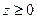 , график расположен выше плоскости
, график расположен выше плоскости 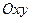 . Его сечения плоскостями
. Его сечения плоскостями
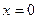 и
и 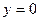 представляют собой полуокружности радиуса 3 с центром в начале координат. «Нижняя» граница графика (пересечение с плоскостью
представляют собой полуокружности радиуса 3 с центром в начале координат. «Нижняя» граница графика (пересечение с плоскостью 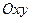 )представляет собой окружность радиуса 3 (рис.15.2).
)представляет собой окружность радиуса 3 (рис.15.2).
б) В этом случае сечения графика плоскостями 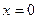 и
и 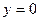 представляют собой параболы с вершиной в точке (0;0;9) и ветвями, направленными вниз. Сечение плоскостью
представляют собой параболы с вершиной в точке (0;0;9) и ветвями, направленными вниз. Сечение плоскостью 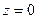 есть окружность с центром в начале координат и радиуса 3. Функция не ограничена снизу. Ее график представлен на рис. 15.3.
есть окружность с центром в начале координат и радиуса 3. Функция не ограничена снизу. Ее график представлен на рис. 15.3.
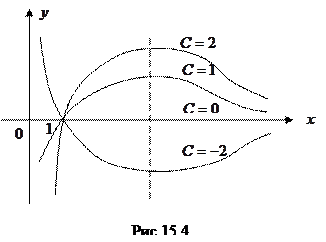 15.3. Построить линии уровня функции
15.3. Построить линии уровня функции 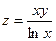 .
.
Решение. Линии уровня имеют вид 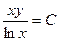 , т.е. представляют собой график функции
, т.е. представляют собой график функции 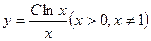 . Функция определена при
. Функция определена при 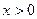 , имеет правостороннюю асимптоту, ось абсцисс, вертикальную асимптоту – ось ординат. Единственная критическая точка
, имеет правостороннюю асимптоту, ось абсцисс, вертикальную асимптоту – ось ординат. Единственная критическая точка 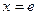 - это точка максимума. Значение функции при этом
- это точка максимума. Значение функции при этом 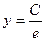 . Таким образом, линии уровня имеют вид, показанный на рис. 15.4.
. Таким образом, линии уровня имеют вид, показанный на рис. 15.4.
15.4. Найти предел 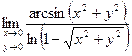
Решение. Обозначим 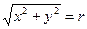 . Тогда условие
. Тогда условие 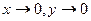 равносильно тому, что
равносильно тому, что 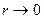 и искомый предел примет вид:
и искомый предел примет вид:
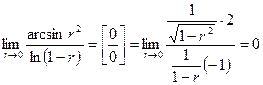 (применили правило Лопиталя).
(применили правило Лопиталя).
15.5. Исследовать на непрерывность в точке (0;0) функцию 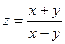 .
.
Решение. Будем приближаться к точке (0;0) по направлению прямых 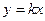 . Тогда будем иметь
. Тогда будем иметь 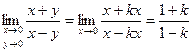 .
.
Значения пределов различны при различных 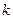 , следовательно, предела функции двух переменных не существует, и функция не является непрерывной в точке (0;0).
, следовательно, предела функции двух переменных не существует, и функция не является непрерывной в точке (0;0).
Найти области определения функций:
15.6. 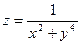 15.7.
15.7. 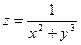 15.8.
15.8. 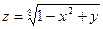
15.9. 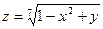 15.10.
15.10. 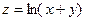 15.11.
15.11. 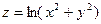
15.12. 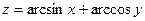 15.13.
15.13. 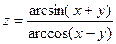 .
.
Найти линии уровня функции в явном виде y = g(x,C):
15.14. 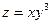 15.15.
15.15. 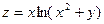 15.16.
15.16. 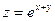
15.17. 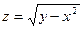 15.18.
15.18. 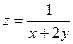 15.19.
15.19. 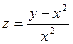
15.20. 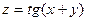
Найти пределы:
15.21.
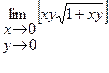
| 15.22. 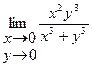
| 15.23. 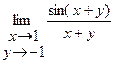
|
15.24.
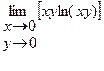
| 15.25. 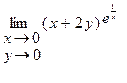
| 15.26. 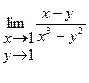
|
15.2. Частные производные, градиент, дифференциал
 2015-03-22
2015-03-22 711
711








