Глава 8.
8.1. Основные теоремы дифференциального исчисления
Краткая теория
1. Теорема Ролля. Пусть функция y = ƒ(x) удовлетворяет следующим условиям:
1) непрерывна на отрезке [a,b];
2) дифференцируема на интервале (a,b);
3) на концах отрезка принимает равные значения, т.е. ƒ(a) = ƒ(b).
Тогда внутри отрезка существует по крайней мере одна такая точка ξ  (a,b), в которой производная равна нулю: ƒ′(ξ) = 0.
(a,b), в которой производная равна нулю: ƒ′(ξ) = 0.
2. Теорема Лагранжа. Пусть функция y = ƒ(x) удовлетворяет следующим условиям:
1) непрерывна на отрезке [a,b];
2) дифференцируема на интервале (a,b).
Тогда внутри отрезка существует по крайней мере одна такая точка ξ  (a,b), в которой выполняется равенство:
(a,b), в которой выполняется равенство:
ƒ′(ξ) = 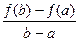 . (8.1)
. (8.1)
8.1. Выяснить, может ли быть применена теорема Лагранжа для функции 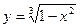 +
+  на отрезке:
на отрезке:
а)  ; б)
; б) 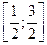 ; в)
; в) 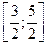 .
.
 2015-03-22
2015-03-22 524
524








