2015-03-22
1103
1. Теорема(правило Лопиталя). Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле:
= 
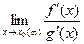. (8.2)
Таким образом, правило Лопиталя используется для раскрытия неопределенностей вида 
или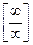 
.
2. Правило Лопиталя можно применять также и для раскрытия неопределенностей вида [0·∞]. Для этого произведение f (x) g (x) следует записать в виде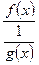 
или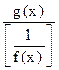 
и получить неопределенность вида или .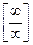
3. Если имеется неопределенность вида [00] или [∞0], при вычислении предела функции f(x)g(x), то логарифм этой функции представляет собой неопределенность вида [0·∞]. При этом используется соотношение (полученное на основе свойств логарифмов и непрерывности показательной функции):
.
8.9. Найти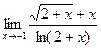 
.
Решение. Так как в данном случае имеется неопределенность вида , можно применить правило Лопиталя (8.2):
= 
= 
= 
.
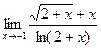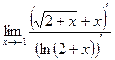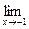
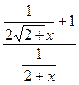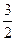8.10. Найти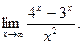 
Решение. Имеет место неопределенность вида 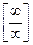. Применяя правило Лопиталя (8.2), получаем: 
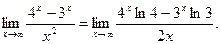Как видим, неопределенность вида 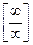остается. Применим правило Лопиталя еще раз.
|
|
|
8.12. Найти предел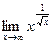 
.
Решение. Имеем неопределенность вида [∞0]. найдем
.
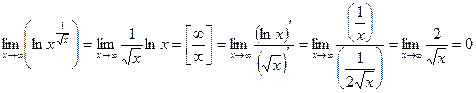По формуле (8.3)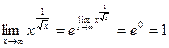 
.
8.13. Найти предел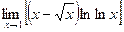 
Решение. Так как при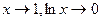 
, то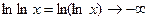 
. Таким образом, имеем неопределенность вида 
.
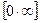Сведем ее к неопределенности вида 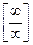и применим правило Лопиталя (8.2):
= 
.
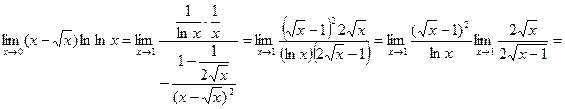
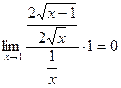8.14. Найти предел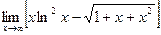 
.
Решение. Имеем неопределенность вида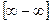 
. Преобразуем искомый предел 
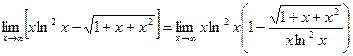и найдем отдельно предел 
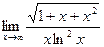, используя правило Лопиталя (8.2):
.
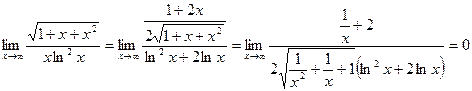Таким образом,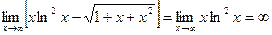 
.
Найти пределы, используя правило Лопиталя:
8.15.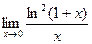 
. 8.16. 
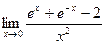. 8.17. 
.
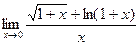8.18.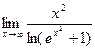 
. 8.19. 
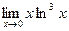. 8.20.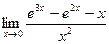 
8.21.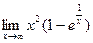 
. 8.22. 
. 8.23.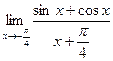 
.
8.24.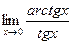 
. 8.25. 
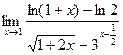. 8.26. 
.
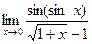8.27.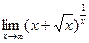 
. 8.28. 
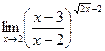. 8.29. 
.
8.30.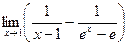 
. 8.31. 
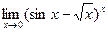. 8.32. 
.
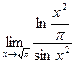8.33.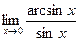 
. 8.34. 
.
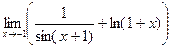8.3. Интервалы монотонности и экстремумы функции
