Решение. а) Имеем показательно-степенную функцию

а) Имеем показательно-степенную функцию. Используя метод логарифмического дифференцирования (7.12) получим:

.

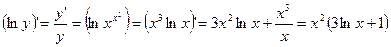Отсюда имеем:

.

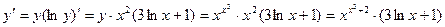б) Здесь заданную функцию также целесообразно прологарифмировать:

.

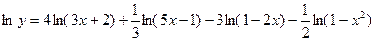Найдем производную:

.

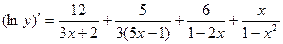Тогда, согласно формуле (7.12), получим

.

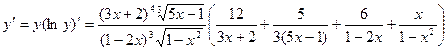6. Найти производную 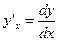неявной функции .

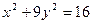Решение. Так как 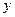является функцией от , то будем рассматривать 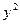как сложную функцию от . Продифференцировав обе части данного уравнения по , имеем

.

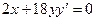Разрешая последнее уравнение относительно 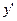, получим:

.

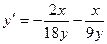7.17. Найти производную 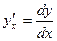функции, заданной параметрически:

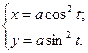
Решение. Используя правила дифференцирования функции, заданной параметрически (7.27), найдем:

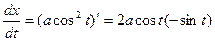и .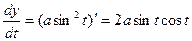

Отсюда .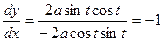

7.18. Найти производную 4-го порядка от функции .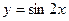

Решение. Последовательно дифференцируя функцию, получим:

; ; ; .

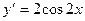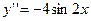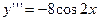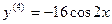7.19. Найти производную второго порядка от функции, заданной параметрически:

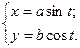
Решение. Последовательно дифференцируя функцию, получим:

;

.

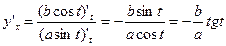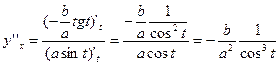7.20. Найти производную n-го порядка от функции .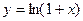

Решение. Последовательно дифференцируя функцию, получим:

; ; ;

; …;

.

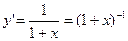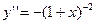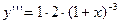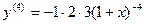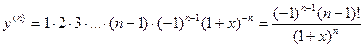Найти производные функций:

7.21. .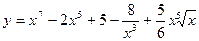

7.27.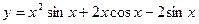

7.29. .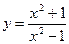

7.35.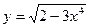

7.45. .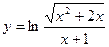

7.49. .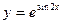

7.57. .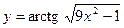

7.65. .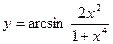

Найти производные 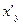обратных функций:

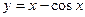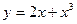7.71. 7.72. 7.75. .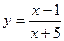

Найти производные 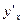от неявных функций:

7.76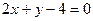

7.77.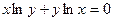

7.79 .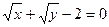

7.82.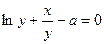

7.84.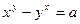

7.85 .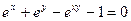

Найти производные функций, заданных параметрически:

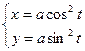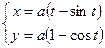7.89. 7.90. 7.91. .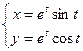

Найти производные второго порядка функций:

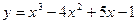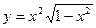7.94 7.95. 7.97. .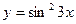

Найти производные 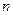-го порядка функций:

7.100. 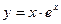7.101. 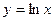7.104. .

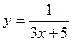7.106. Показать, что функция 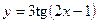удовлетворяет уравнению .

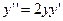7.107. Показать, что функция 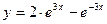удовлетворяет уравнению .

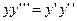7.108. Показать, что функция 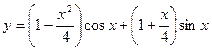удовлетворяет уравнению .

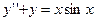7.3. Геометрические и механические приложения производной