1. Предельные величины. Применение производной в экономике позволяет получать так называемые предельные характеристики экономических объектов или процессов. Предельные величины (предельная выручка, полезность, производительность, предельный доход, продукт и др.) характеризуют не состояние, а скорость изменения экономического объекта или процесса по времени или относительно другого исследуемого фактора.
Издержки производства. Если издержки производства 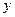 рассматривать как функцию выпускаемой продукции
рассматривать как функцию выпускаемой продукции  , т.е.
, т.е. 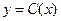 , то
, то 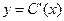 будет выражать предельные издержки производства и приближенно характеризовать прирост переменных затрат на производство дополнительной единицы продукции. Средние издержки являются издержками на единицу выпуска продукции:
будет выражать предельные издержки производства и приближенно характеризовать прирост переменных затрат на производство дополнительной единицы продукции. Средние издержки являются издержками на единицу выпуска продукции: 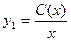 .
.
2. Производительность труда. Пусть функция 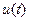 выражает объем произведенной продукции
выражает объем произведенной продукции 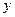 за время
за время 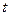 . Тогда производная объема произведенной продукции по времени
. Тогда производная объема произведенной продукции по времени 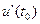 есть производительность труда в момент
есть производительность труда в момент 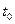 .
.
3. Функция потребления и сбережения. Если  - национальный доход,
- национальный доход, 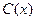 - функция потребления (часть дохода, которая тратится), а
- функция потребления (часть дохода, которая тратится), а 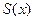 - функция сбережения, то
- функция сбережения, то
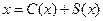 . (7.33)
. (7.33)
Дифференцируя, получим, что
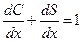 , (7.34)
, (7.34)
где 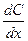 - предельная склонность к потреблению;
- предельная склонность к потреблению; 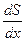 - предельная склонность к сбережению.
- предельная склонность к сбережению.
4. Эластичность. Эта мера реагирования одной переменной величины на изменение другой. Эластичность функции приближенно показывает, на сколько процентов изменится одна переменная в результате изменения другой переменной на 1%.
Эластичность функции определяется с помощью соотношения:
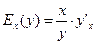 или
или 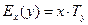 , (7.35)
, (7.35)
где
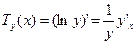 (7.36)
(7.36)
– относительная скорость изменения (темп) функции.
Эластичность функции применяется при анализе спроса и предложения от цены (ценовая эластичность). Она показывает реакцию спроса или предложения на изменение цены и определяет, на сколько процентов приближенно изменится спрос или предложение при изменении цены на 1%.
Если эластичность спроса 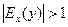 , то спрос считается эластичным, если
, то спрос считается эластичным, если 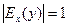 – нейтральным (с единичной эластичностью), а если
– нейтральным (с единичной эластичностью), а если 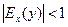 – неэластичным относительно цены.
– неэластичным относительно цены.
7.131. Функция издержек производства продукции некоторой фирмой имеет вид: 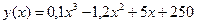 (ден. ед.). Найти средние и предельные издержки производства и вычислить их значение при
(ден. ед.). Найти средние и предельные издержки производства и вычислить их значение при 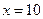 .
.
Решение. Найдем производную 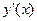 и ее значение
и ее значение 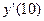 - предельные издержки производства:
- предельные издержки производства:
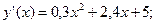
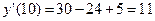 .
.
Средние издержки:
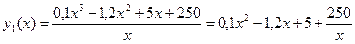 ;
;
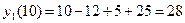 .
.
Это означает, что при данном уровне производства (количестве выпускаемой продукции) средние затраты на производство одной единицы продукции составляют 28 ден. ед., а увеличение объема на одну единицу продукции обойдется фирме приближенно в 11 ден. ед.
7.132. Функция потребления некоторой страны имеет вид:
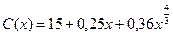 ,
,
где  - совокупный национальный доход (ден. ед.). Найти: а) предельную склонность к потреблению; б) предельную склонность к сбережению, если национальный доход составляет 27 ден. ед.
- совокупный национальный доход (ден. ед.). Найти: а) предельную склонность к потреблению; б) предельную склонность к сбережению, если национальный доход составляет 27 ден. ед.
Решение: Предельная склонность к потреблению: 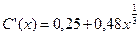 ; ее значение:
; ее значение: 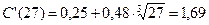 .
.
Предельная склонность к сбережению:
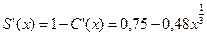 ; ее значение:
; ее значение: 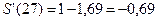 .
.
7.133. Объем производства зимней обуви 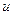 , выпускаемый некоторой фирмой, может описан уравнением
, выпускаемый некоторой фирмой, может описан уравнением 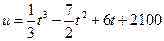 (ед), где
(ед), где 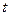 - календарный месяц года. Вычислить производительность труда, скорость и темп ее изменения: а) в начале года (
- календарный месяц года. Вычислить производительность труда, скорость и темп ее изменения: а) в начале года (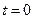 ); б) в середине года (
); б) в середине года (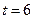 ); в) в конце года (
); в) в конце года (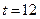 ).
).
Решение. Производительность труда выражается производной 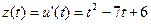 (ед./мес.), а скорость и темп изменения производительности – соответственно производной
(ед./мес.), а скорость и темп изменения производительности – соответственно производной 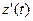 и логарифмической производной
и логарифмической производной 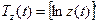 :
: 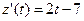 (ед./мес.2),
(ед./мес.2), 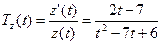 (ед./мес.).
(ед./мес.).
В заданные моменты времени соответственно имеем 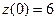 (ед./мес.),
(ед./мес.), 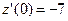 (ед./мес2.),
(ед./мес2.), 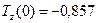 (ед./мес.),
(ед./мес.), 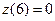 (ед./мес.),
(ед./мес.), 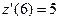 (ед./мес2.),
(ед./мес2.), 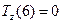 (ед./мес.),
(ед./мес.), 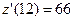 (ед./мес.2),
(ед./мес.2), 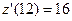 (ед./мес.2),
(ед./мес.2), 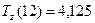 (ед./мес.).
(ед./мес.).
7.134. Функция спроса 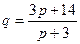 и предложение
и предложение 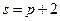 , где
, где 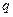 и
и 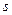 - количество товаров, соответственно покупаемого и предлагаемого на продажу в единицу времени,
- количество товаров, соответственно покупаемого и предлагаемого на продажу в единицу времени, 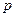 - цена единицы товара. Найти: а) равновесную цену, то есть цену, при которой спрос и предложение уравновешиваются; б) эластичность спроса и предложения; в) изменение дохода при увеличении цены на 10% от равновесной.
- цена единицы товара. Найти: а) равновесную цену, то есть цену, при которой спрос и предложение уравновешиваются; б) эластичность спроса и предложения; в) изменение дохода при увеличении цены на 10% от равновесной.
Решение: а) Равновесная цена определяется из условия 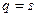 , т.е.
, т.е. 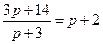 ; откуда
; откуда 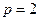 , т.е. равновесная цена равна 2 ден. ед.
, т.е. равновесная цена равна 2 ден. ед.
б) Найдем эластичности по спросу и предложению по формуле (7.35):
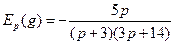 ;
; 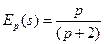 .
.
Для равновесной цены 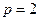 имеем
имеем 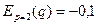 ;
; 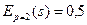 .
.
Так как полученные значения эластичности меньше 1 (по абсолютной величине), то спрос и предложение данного товара при равновесной (рыночной) цене неэластичны относительно цены. Это означает, что изменение цены не приведет к резкому изменению спроса и предложения.
в) При увеличении цены 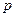 на 10% от равновесной спрос уменьшается на
на 10% от равновесной спрос уменьшается на 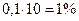 , следовательно, доход
, следовательно, доход 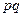 возрастает приближенно на 9%.
возрастает приближенно на 9%.
7.135. Зависимость между спросом 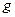 и ценой
и ценой 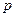 за единицу продукции, выпускаемой некоторым предприятием, дается соотношением
за единицу продукции, выпускаемой некоторым предприятием, дается соотношением 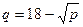 . Найти эластичность спроса. Выяснить, при каких значениях цены спрос является эластичным, нейтральным и неэластичным. Какие рекомендации о цене за единицу продукции можно дать руководителям предприятия при
. Найти эластичность спроса. Выяснить, при каких значениях цены спрос является эластичным, нейтральным и неэластичным. Какие рекомендации о цене за единицу продукции можно дать руководителям предприятия при 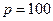 и при
и при 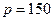 ден. ед.?
ден. ед.?
Решение. Эластичность спроса по формуле (7.35) есть 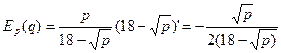 .
.
Спрос нейтрален, если 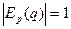 . Решая это уравнение, имеем
. Решая это уравнение, имеем 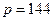 . Далее, принимая во внимание, что
. Далее, принимая во внимание, что 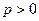 и
и 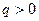 (т.е.
(т.е. 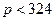 ), получим, что если
), получим, что если 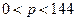 - спрос является неэластичным; при
- спрос является неэластичным; при 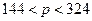 - спрос эластичен.
- спрос эластичен.
Рекомендации. Если цена единицы продукции составляет 100 ден. ед., то спрос является неэластичным и можно повысить цену продукции, выручка при этом будет расти. При стоимости продукции 150 ден. ед. спрос является эластичным. В данном случае целесообразно рассмотреть предложение о снижении цены, выручка от реализации будет расти в результате увеличения спроса на продукцию.
7.136. Задана функция 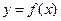 полных затрат предприятия на производство
полных затрат предприятия на производство  единиц продукции. Определить связь между коэффициентом эластичности полных и средних затрат.
единиц продукции. Определить связь между коэффициентом эластичности полных и средних затрат.
Решение. Средние затраты на единицу продукции равны: 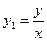 . По формуле (7.35.) коэффициенты эластичности полных и средних затрат равны:
. По формуле (7.35.) коэффициенты эластичности полных и средних затрат равны: 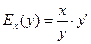 ;
;
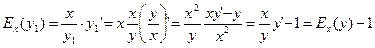 , т.е. коэффициент эластичности средних затрат на единицу меньше коэффициента эластичности полных затрат.
, т.е. коэффициент эластичности средних затрат на единицу меньше коэффициента эластичности полных затрат.
7.137. Зависимость между издержками производства и объемом выпускаемой продукции  на предприятии выражается функцией
на предприятии выражается функцией 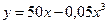 . Определить средние и предельные издержки при объеме продукции 10 ед.
. Определить средние и предельные издержки при объеме продукции 10 ед.
7.138. Выручка от продажи конфет составляет 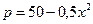 , где
, где  - объем проданной продукции (тыс. ед.). Найти среднюю и предельную выручку, если продано: а) 10 тыс. ед.; б) 60 тыс. ед.
- объем проданной продукции (тыс. ед.). Найти среднюю и предельную выручку, если продано: а) 10 тыс. ед.; б) 60 тыс. ед.
7.139. Функция издержек производства 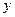 от объема выпускаемой продукции
от объема выпускаемой продукции  имеет вид
имеет вид 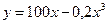 . Определить средние и предельные издержки при объеме продукции 10 ед.
. Определить средние и предельные издержки при объеме продукции 10 ед.
7.140. Себестоимость продукции 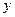 связана с объемом выпускаемой продукции
связана с объемом выпускаемой продукции  уравнением:
уравнением: 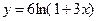 . Определить среднюю и предельную себестоимость выпускаемой продукции при объеме, равной 10 ед.
. Определить среднюю и предельную себестоимость выпускаемой продукции при объеме, равной 10 ед.
7.141. Производительность труда бригады может описана уравнением 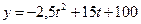 , где
, где 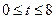 - рабочее время в часах. Вычислить скорость и темп изменения производительности труда при
- рабочее время в часах. Вычислить скорость и темп изменения производительности труда при 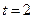 и
и 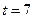 .
.
7.142. Себестоимость производства телевизоров 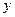 (в тыс. руб.) описывается функцией
(в тыс. руб.) описывается функцией 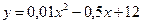 ,
,  , где
, где  - объем выпускаемой продукции в месяц (тыс. ед.). Определить скорость и темп изменения себестоимости и при выпуске 20 и 40 тыс. ед. продукции.
- объем выпускаемой продукции в месяц (тыс. ед.). Определить скорость и темп изменения себестоимости и при выпуске 20 и 40 тыс. ед. продукции.
7.143. Функция потребления некоторой страны имеет вид: 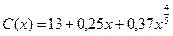 , где
, где  - совокупный национальный доход. Найти: а) предельную склонность к потреблению; б) предельную склонность к сбережению, если национальный доход составляет 32.
- совокупный национальный доход. Найти: а) предельную склонность к потреблению; б) предельную склонность к сбережению, если национальный доход составляет 32.
7.144. Функция потребления некоторой страны имеет вид: 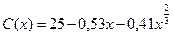 , где
, где  - совокупный национальный доход. Найти: а) предельную склонность к потреблению; б) предельную склонность к сбережению, если национальный доход составляет 27.
- совокупный национальный доход. Найти: а) предельную склонность к потреблению; б) предельную склонность к сбережению, если национальный доход составляет 27.
7.145. Зависимость между себестоимостью готовой продукции предприятия 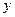 (млн. руб.) и объемом выпускаемых изделий
(млн. руб.) и объемом выпускаемых изделий  (тыс. шт.) выражается уравнением
(тыс. шт.) выражается уравнением 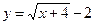 . Найти эластичность себестоимости продукции предприятия, выпускающего 12 тыс. шт. изделий. Какие рекомендации можно дать руководителям предприятия об изменении величины объема выпускаемой продукции?
. Найти эластичность себестоимости продукции предприятия, выпускающего 12 тыс. шт. изделий. Какие рекомендации можно дать руководителям предприятия об изменении величины объема выпускаемой продукции?
7.146. Функция полных затрат в зависимости от объема выпускаемой продукции задана соотношением: 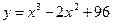 . При каком объеме производства предельные и средние затраты совпадают? Найти коэффициенты эластичности полных и средних затрат при данном объеме.
. При каком объеме производства предельные и средние затраты совпадают? Найти коэффициенты эластичности полных и средних затрат при данном объеме.
7.147. Зависимость между объемом выпуска готовой продукции 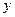 (млн. руб.) и объемом производственных фондов
(млн. руб.) и объемом производственных фондов  (млн. руб.) выражается уравнением
(млн. руб.) выражается уравнением 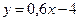 . Найти эластичность выпуска продукции для предприятия, имеющего фонды в размере 40 млн. руб.
. Найти эластичность выпуска продукции для предприятия, имеющего фонды в размере 40 млн. руб.
7.148. Зависимость между себестоимостью единицы продукции 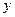 (в руб.) и выпуском продукции
(в руб.) и выпуском продукции  (в млн. руб.) выражается уравнением
(в млн. руб.) выражается уравнением 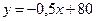 . Найти эластичность себестоимости при выпуске продукции на 30 млн. руб.
. Найти эластичность себестоимости при выпуске продукции на 30 млн. руб.
7.149. Зависимость между количеством выпускаемых деталей в партии  (тыс. ед.) и затратами на их изготовление
(тыс. ед.) и затратами на их изготовление 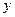 (тыс. руб.) для предприятия отрасли выражается уравнением
(тыс. руб.) для предприятия отрасли выражается уравнением 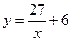 . Найти эластичность затрат для предприятий, выпускающих по 10 тыс. деталей в партии.
. Найти эластичность затрат для предприятий, выпускающих по 10 тыс. деталей в партии.
7.150. Найти эластичность функции спроса при заданной стоимости 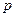 :
:
а) 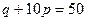 ,
, 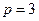 ; б)
; б)  ,
, 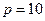 ; в)
; в) 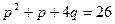 ,
, 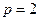 и
и 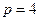 .
.
7.151. Для следующих функций спроса найти значение 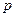 , при которых спрос является эластичным: а)
, при которых спрос является эластичным: а) 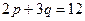 ; б)
; б) 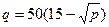 ; в)
; в) 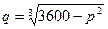 .
.
7.152. Задана функция спроса 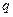 и предложения
и предложения 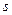 от цены
от цены  :
: 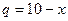 ,
, 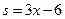 . Найти: а) равновесную цену; б) эластичность спроса и предложения для равновесной цены; в) изменение дохода при изменении равновесной цены на 5 %.
. Найти: а) равновесную цену; б) эластичность спроса и предложения для равновесной цены; в) изменение дохода при изменении равновесной цены на 5 %.
7.153. Функции спроса 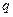 и предложения
и предложения  на некоторый товар от его цены
на некоторый товар от его цены  задаются уравнениями:
задаются уравнениями: 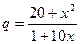 ,
, 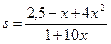 . Найти: а) равновесную цену; б) эластичность спроса и предложения для равновесной цены; в) изменение дохода при изменении равновесной цены на 5 %.
. Найти: а) равновесную цену; б) эластичность спроса и предложения для равновесной цены; в) изменение дохода при изменении равновесной цены на 5 %.
7.154. Зависимость потребления 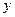 от дохода
от дохода  задается функцией
задается функцией 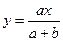 . Показать, что эластичность функции потребления от дохода не зависит от параметра
. Показать, что эластичность функции потребления от дохода не зависит от параметра 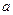 и стремится к нулю при неограниченном возрастании дохода.
и стремится к нулю при неограниченном возрастании дохода.
 2015-03-22
2015-03-22 7089
7089