1) Ширина спектральной плотности и корреляционной функции связаны обратной зависимостью: чем шире корреляционная функция (больше время корреляции), тем уже спектральная плотность, и наоборот.
2) Спектральная функция является четной функцией:
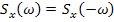
3) Спектральная плотность белого шума:
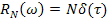
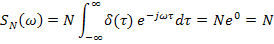
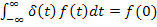
Спектральная плотность постоянна на всех частотах. Мощность белого шума распространяется равномерно на всей частотной оси. Поэтому шум называется «белым», по аналогии с «белым светом».
4) Спектральная плотность постоянного сигнала 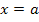
Поскольку интеграл Фурье при постоянном значении подынтегральной функции не сходится (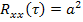 ), то спектральная плотность находится из обратного преобразования:
), то спектральная плотность находится из обратного преобразования:
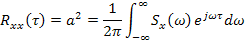
Для того, чтобы интеграл дал постоянную величину, необходимо, чтобы подынтегральная функция была равна 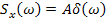 .
.
Тогда 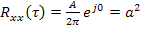
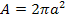 и
и 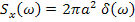 .
.
5) Спектральная плотность гармонической функции
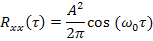
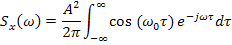
Так же, как и в предыдущем случае, в связи с тем, что интеграл не сходится, находим спектральную плотность через обратное преобразование Фурье:
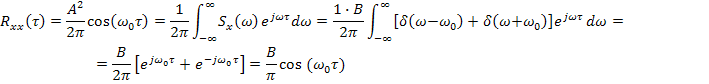
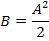
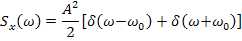
 2015-03-22
2015-03-22 388
388








