Расчет ошибки регулирования при случайных возмущающих воздействий в линейной системе

Wp(p)

g(t)

e(t)

z(t)

y(t)

В общем случае случайные процессы g(t) и z(t) могут быть коррелированными или некоррелированными.

Требуется определить параметры ошибки регулирования, которая также будет случайным процессом.

Точка приложения возмущения может быть в любом месте.

Наиболее часто в качестве показателя ошибки используется среднеквадратичное значение или средний квадрат ошибки.

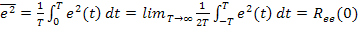- значение корреляционной функции для ошибки при t=0.

.

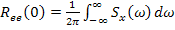Как видно, для определения среднего квадрата ошибки необходимо получить спектральную плотность ошибки.

Для коррелированных процессов g(t) и z(t) спектральная плотность ошибки определяется как:

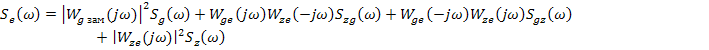
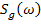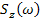, - спектральные плотности процессов g(t) и z(t),

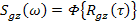- взаимные спектральные плотности процессов g(t) и z(t),

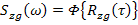
Соответственно 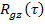и 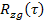- взаимные корреляционные функции процессов,

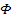- операция преобразования Фурье,

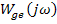и 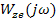- комплексные частотные характеристики замкнутой системы от входов g и z к выходу е.

Для некоррелированных случайных процессов g и z:

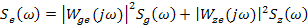
Взаимные корреляционные функции для некоррелированных случайных процессов равны 0.

Средний квадрат ошибки равен

.

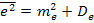Для того, чтобы определить отдельно математическое ожидание и дисперсию случайного процесса е(t), можно представить входные процессы g(t) и z(t) в виде сумм центрированных процессов и их математических ожиданий, которые для стационарных процессов имеют вид:

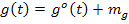
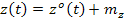
Учитывая принцип суперпозиции для линейных систем, а также невозможность возникновения в линейной системе новых гармоник можно отдельно рассмотреть прохождение через линейную систему центрированных процессов и постоянных сигналов, равных математическим ожиданиям. Тогда

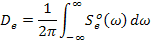
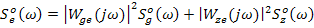
Математическое ожидание ошибки при постоянных входных воздействиях можно считать равным установившейся ошибке:

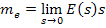
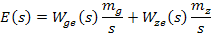
Аналогичным образом можно получить параметры любого промежуточного сигнала в системе, используя спектральную плотность входных сигналов и передаточные функции элементов системы.

Зачастую при аналитических исследованиях прохождения случайных процессов для описания корреляционных функций используют аппроксимирующие их выражения.