На вход линейного звена подается случайный процесс. Если рассматривать случайный процесс как сумму центрированного процесса и математического ожидания, то в соответствии с принципом суперпозиции можно отдельно преобразовать функцию математического ожидания и центрированный случайный процесс, а затем их просуммировать.
Если корреляционная функция случайного процесса на входе 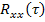 , то для эргодического процесса корреляционная функция на выходе:
, то для эргодического процесса корреляционная функция на выходе:
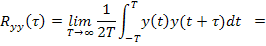
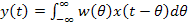 ,
,
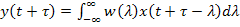 ,
,
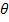 ,
, 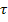 ,
, 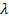 - время.
- время.
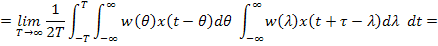
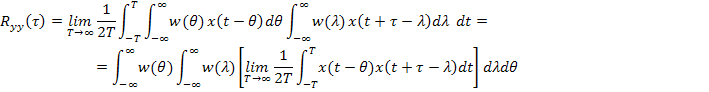
Выражение в квадратных скобках является фактически корреляционной функцией входного процесса x для смещения 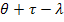 .
.
Тогда корреляционная функция
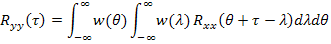
Если входным процессом является «белый шум» 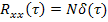 , то корреляционная функция процесса на выходе будет:
, то корреляционная функция процесса на выходе будет:
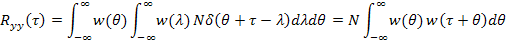
Спектральная плотность случайного процесса на выходе линейного звена:
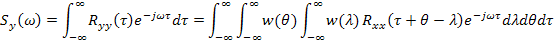
Если экспоненту 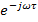 умножить на
умножить на 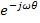 и
и 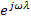 , то:
, то:
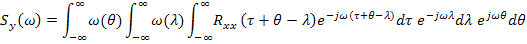
Самый внутренний интеграл (по 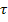 ) является фактически преобразованием Фурье от корреляционной функции входного процесса, поскольку смещение аргумента на величину
) является фактически преобразованием Фурье от корреляционной функции входного процесса, поскольку смещение аргумента на величину 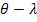 не изменяет интеграл для бесконечных пределов интегрирования, т.е.:
не изменяет интеграл для бесконечных пределов интегрирования, т.е.:
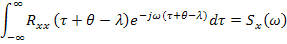
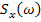 не зависит от
не зависит от 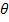 и
и 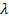 и может быть вынесено из под интеграла.
и может быть вынесено из под интеграла.
Оставшийся двойной интеграл от 2-х независимых аргументов распадается на произведение 2-х интегралов:
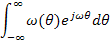
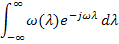
Эти интегралы фактически являются преобразованием Фурье от весовой функции, т.е. комплексной частотной характеристикой, причем 1-й можно считать для отрицательной частоты 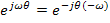 , а второй – для положительной:
, а второй – для положительной:
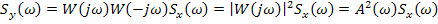
Если на вход линейного звена подается «белый шум» со спектральной плотностью 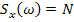 , то на выходе
, то на выходе 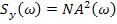 .
.
 2015-03-22
2015-03-22 1321
1321
