Свойства корреляционных функций

1)

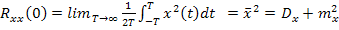
2)

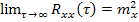
Если записать классическое выражение для корреляционной функции:

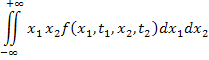
для большого интервала времени τ= 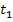- 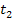2-мерная плотность распределения вероятности равна произведению одномерных плотностей

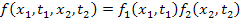
т.к. значения процессов 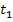и 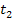не зависят друг от друга, и тогда интеграл распадается на два

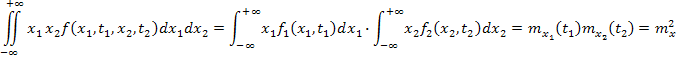
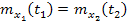, т.к. случайный процесс стационарный.

3) Значение корреляционной функции для 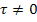не будет превышать значения 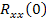, т.е. корреляционная функция, как правило, убывает при увеличении t.

Зачастую для аппроксимации корреляционных функций используют выражение:

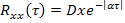
Для колебательных корреляционных функций

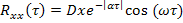
4) Корреляционная функция является четной функцией:

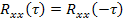
5) Корреляционная функция суммы 2-х случайных процессов 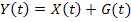равна:

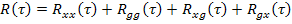
6) Корреляционная функция белого шума интенсивностью N определяется т.о.:

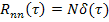
7) Время корреляции определяется как минимальное время, при котором было достигнуто неравенство: .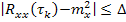

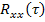
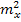
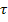
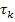
8) Зачастую формулу для вычисления корреляционной функции чисто формально применяют к неслучайным (детерминированным) процессам.

9) Корреляционная функция от постоянной величины .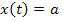

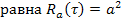10) Если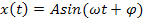

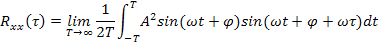
Для интеграла интервал интегрирования можно брать равным периоду колебания.

,

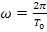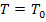
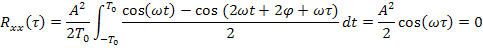
Если случайный процесс представить в виде суммы гармонических функций (разложение в ряд Фурье), то получим набор гармоник с частотой изменения от 0 до предельной.

Коэффициенты Фурье будут случайными значениями, а частоты – заданными (детерминированными). Тогда корреляционная функция такого случайного процесса может быть представлена:

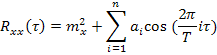
где 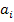- коэффициенты ряда Фурье.