Необходимо синтезировать замкнутую систему, изменяющую координату объекта y(t) в соответствии с законом
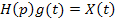
где 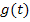 - входное воздействие,
- входное воздействие, 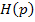 – некоторый оператор,
– некоторый оператор,
причем 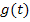 - случайный процесс.
- случайный процесс.
Система подвергнута случайному возмущающему воздействию 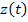 , которое в общем случае может быть коррелированно с
, которое в общем случае может быть коррелированно с 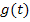 .
.
Считаем, что 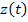 приведено ко входу системы (смотри методы переноса сигнала по системе). Синтез замкнутой системы проводим из условия обеспечения минимума среднего квадрата ошибки:
приведено ко входу системы (смотри методы переноса сигнала по системе). Синтез замкнутой системы проводим из условия обеспечения минимума среднего квадрата ошибки:
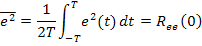
| Wз(p) |
| z(t) |
| g(t) |
| y(t) |
Необходимо при синтезе определить оптимальную передаточную функцию замкнутой системы, включающую объект и формирователь управляющего воздействия, а также датчики и исполнительные механизмы, из условия обеспечения минимума 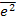 .
.
Для этой системы
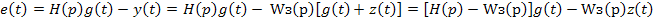
В этом случае
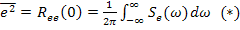
Спектральная плотность ошибки для некоррелированных воздействий равна:
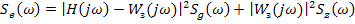
где 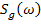 и
и 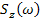 - спектральные плотности входных воздействий.
- спектральные плотности входных воздействий.
При суммировании или вычитании случайных процессов спектральные плотности суммируются.
Задача – найти такую 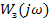 , чтобы интеграл
, чтобы интеграл 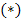 был минимальным.
был минимальным.
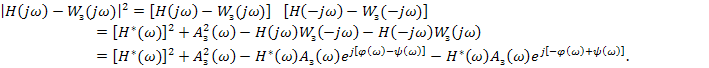
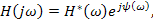
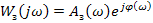
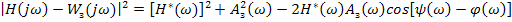
В связи с тем, что под интегралом 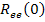 стоит сумма положительных функций, минимум интеграла будет в случае, когда каждая функция будет минимально возможной.
стоит сумма положительных функций, минимум интеграла будет в случае, когда каждая функция будет минимально возможной.
Слагаемое 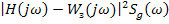 будет минимальным в случае, когда произведение
будет минимальным в случае, когда произведение 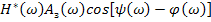 будет максимальным, т.к. перед ним стоит «-».
будет максимальным, т.к. перед ним стоит «-».
Это выражение будет максимальным, если 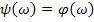 , т.е. фазовые характеристики r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
, т.е. фазовые характеристики r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 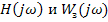 совпадают.
совпадают.
При этом условии спектральная плотность ошибки 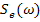 будет иметь вид:
будет иметь вид:
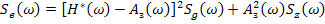
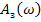 , обеспечивающее минимум заведомо положительной функции
, обеспечивающее минимум заведомо положительной функции 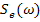 , может быть найдена из уравнения:
, может быть найдена из уравнения:
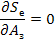
Дифференцируем функцию по функции 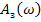 :
:
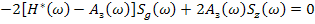
Отсюда:
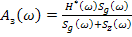
С учетом равенства фазовых характеристик получаем:
 – передаточная функция замкнутой оптимальной системы.
– передаточная функция замкнутой оптимальной системы.
Для коррелированных случайных процессов оптимальная передаточная функция замкнутой системы:
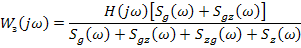
Проблема заключается в том, что полученная т.о. оптимальная передаточная функция крайне редко может быть реализована. Это связано с тем, что отдельно формировались условия для получения фазовой и амплитудной частотных характеристик системы, а они связаны друг с другом.
Например, если синтезируется система регулирования, для которой 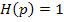 ,
, 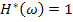 ,
, 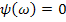 , то
, то
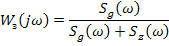
Как видно, частотная характеристика получилась действительной, зависящей от 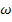 .
.
Т.к. частотная характеристика есть преобразование Фурье от весовой функции, то вещественной (действительной) частотной характеристике соответствует симметричная относительно оси ординат весовая функция, т.е. функция, не равная 0 для отрицательного времени. а поскольку весовая функция есть реакция системы на 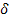 - импульс при нулевых начальных условиях, то это означает, что реакция системы возникает до поступления
- импульс при нулевых начальных условиях, то это означает, что реакция системы возникает до поступления 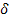 – импульса, что не реально. Вещественная функция
– импульса, что не реально. Вещественная функция 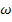 может быть получена путем перемножения комплексно- сопряженных функций, т.е. функций, зависящих от
может быть получена путем перемножения комплексно- сопряженных функций, т.е. функций, зависящих от 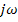 и
и 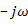 .
.
Одна из таких методик получения квазиоптимальных передаточных функций, предложена Боде и Шенноном.
 2015-03-22
2015-03-22 388
388








