Для коррелированных Марковских центрированных случайных процессов g и f стационарное уравнение для определения квазиоптимальной передаточной функции замкнутой системы, обеспечивающей минимум среднего квадрата ошибки, имеет вид:
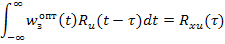
где 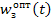 - весовая функция замкнутой системы.
- весовая функция замкнутой системы.
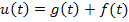
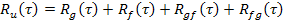
- взаимная корреляционная функция для воздействий,
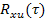 – взаимная корреляционная функция отрабатываемого сигнала
– взаимная корреляционная функция отрабатываемого сигнала 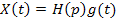 и сигнала
и сигнала 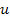 .
.
Это уравнение носит название Винера-Хопфа.
Частотная характеристика реализуемой системы получается следующим путем:
Из преобразований Фурье
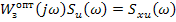
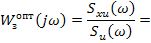
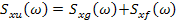
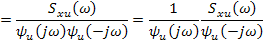
Чтобы получить реализуемую частотную характеристику от 2-го сомножителя, выполнили обратное преобразование Фурье, умножили на единичную ступенчатую функцию (весовая функция реальной системы должна быть равна 0 при 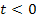 ).
).
Выполним снова преобразование Фурье, получим формулу Винера:
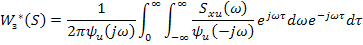
 2015-03-22
2015-03-22 1089
1089








