Методика Боде-Шеннона

Рассмотрим на примере:

Пусть на вход системы воздействуют случайные процессы 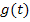с корреляционной функцией

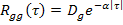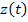и с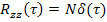

Корреляционную функцию 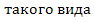имеет, в частности, случайный процесс, у которого моменты изменения и уровни случайны.

t₁ t

Требуется получить квазиоптимальные передаточные функции замкнутой и разомкнутой систем регулирования из условий минимума среднеквадратичной ошибки.

Спектральные плотности

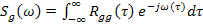
Т.к. корреляционная функция нелинейная по времени, разделим интервал интегрирования на отрицательный (по времени) и положительный:

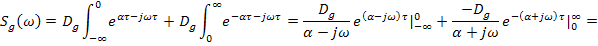
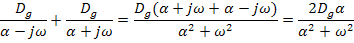
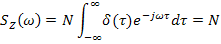
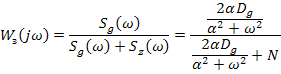
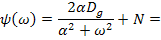
1 этап. В соответствии с методикой Боде-Шеннона на 1-м этапе осуществляют расщепление (факторизацию) знаменателя частотной характеристики на комплексно сопряженные функции.

Факторизация – представление знаменателя частотной характеристики
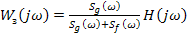в виде произведения комплексно сопряженных функций:

,

,

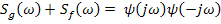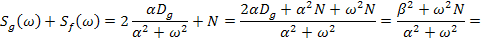
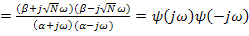где , , .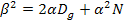

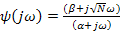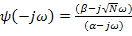2 этап. Разделение, или сепарирование.

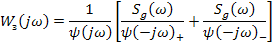
Слагаемое в квадратных скобках со знаком «+» представляет собой реализуемую часть, а со знаком «-» - нереализуемую.

Для рассматриваемого примера

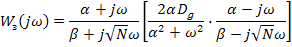
произведение в скобках может быть преобразовано к следующему виду:

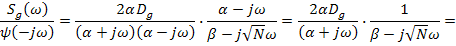
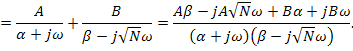
Сравнивая числители из равенства: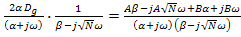

получаем уравнение для нахождения A и B.

,

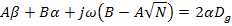
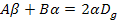
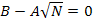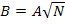
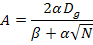
3. Отбрасывая нереализуемую часть 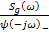, получаем квазиоптимальную передаточную функцию:

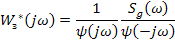
В примере отбрасываем 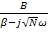и получаем

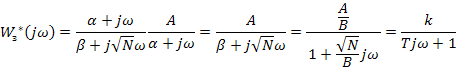
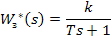
4. Чтобы найти передаточную функцию формирователя управляющего воздействия, необходимо получить передаточную функцию разомкнутой системы.

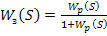- при отрицательной единичной обратной связи

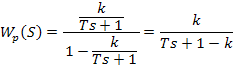
Делим числитель и знаменатель на (1-k):

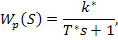
где , .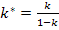

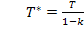Имея передаточную функцию разомкнутой системы, можно найти передаточную функцию формирователя.

Для коррелированных сигналов g и f:

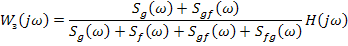
Для марковских случайных процессов (таких процессов, у которых информация о возможных последующих изменениях процесса содержится только в предыдущий момент времени) теория оптимальной фильтрации в спектральной области разработана Калманом.

Для обычных случайных процессов накопление информации с ходом времени позволяет прогнозировать изменение процесса в будущем, причем с увеличением интервала наблюдения достоверность прогноза увеличивается, у марковских процессов это свойство отсутствует, примером таких процессов является «белый шум»).