2015-03-22
618
Система или объект, имеющие больше одного управляемого выхода, называются многомерными, или многосвязными.
|
|
|
|
|
|
-
-
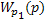
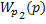
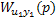
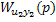
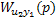
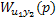
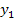
В общем случае дифференциальное уравнение, описывающее динамику многомерного объекта, имеет вид:
…
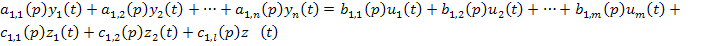
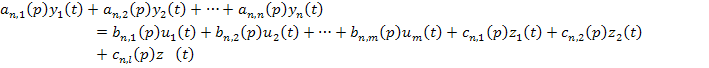
где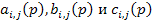 
- полиномы соответствующих степеней.
Пример:
, 
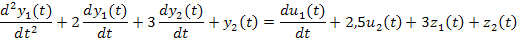
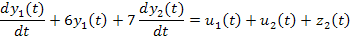
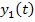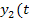) – управляемые параметры объекта,
, 
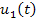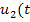) - управляющие воздействия,
, 
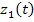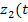)- возмущения.
В матричной форме исходную систему можно записать:
,
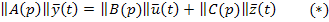s w:val="24"/></w:rPr></m:ctrlPr></m:dPr><m:e><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>B(p)</m:t></m:r></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">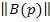 
и s w:val="24"/></w:rPr></m:ctrlPr></m:dPr><m:e><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>C(p)</m:t></m:r></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
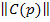- матрицы многочленов,
, 
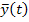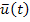и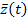 
- векторы управляемых параметров, управлений и возмущений.
Для приведенного примера:
, 
, 
, 
, 
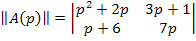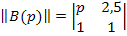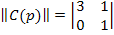
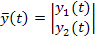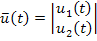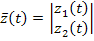
Если умножить левую и правую части уравнения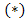 
на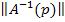 
, то получим:
,
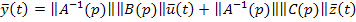
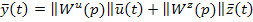где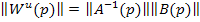 
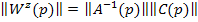
Так же, как и в одномерных системах, записываются передаточные функции в преобразованиях Лапласа. Для этого дифференциальное уравнение в матричной форме преобразуется по Лапласу (для нулевых начальных условий) и определяется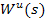 
.
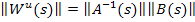
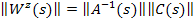
Матрица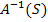 
определяется т.о.:
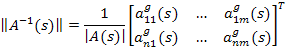
где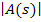 
– определитель матрицы 
,
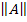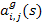- алгебраические дополнения к элементу 
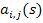в матрице ,
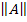Т – символ транспонирования матрицы.
Пример
Объект, зависящий от 2-х воздействий, и 2-х управляющих координат:
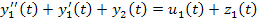
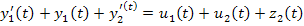
В преобразованиях Лапласа для нулевых начальных условий:
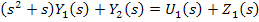
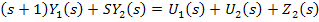
Если записать в матричной форме:
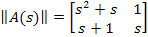
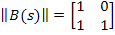
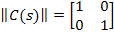
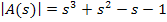
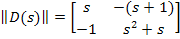
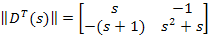
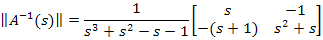
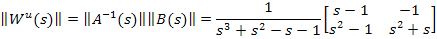
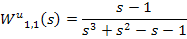
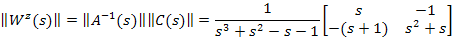
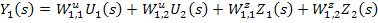
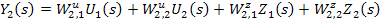
Поскольку интеграл от матрицы равен матрице интегралов, а весовая функция определяется обратным преобразованием Лапласа от передаточной функции, т.е. путем интегрирования матрицы передаточных функций, умноженной на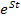 
, так же, как и матрица передаточных функций существует матрица весовых функций
