При синтезе нелинейных систем возникают следующие ситуации:
1) Система синтезируется как линейная, а нелинейности компенсируются дополнительными звеньями, включаемыми обычно последовательно с нелинейным звеном.
Если 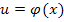 , где
, где 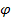 – непрерывная однозначная нелинейность, то включают последовательно с нелинейным звено
– непрерывная однозначная нелинейность, то включают последовательно с нелинейным звено 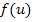 , такого типа, чтобы сигнал
, такого типа, чтобы сигнал 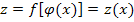 стал линейно зависящим от
стал линейно зависящим от 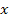 .
.
Прием называется компенсацией нелинейности.
При использовании вычислительных устройств, нелинейности (от датчиков) компенсируются расчетным путем.
U U
x x
Если нелинейные элементы имеют зону нечувствительности (зачастую это относится к датчикам перемещения или вращения механического типа), то для устранения этих зон нечувствительности используют метод вибрационной линеаризации.
2) Если нелинейности являются существенными и некомпенсируемыми, то применяются либо приближенные методы для синтеза систем, либо специальные, учитывающие особенности нелинейности.
3) В ряде случаев нелинейное устройство вводят специально для получения оптимальных в смысле определенного критерия систем. Известен широкий класс нелинейных систем – систем с переменной структурой, когда закон управления изменяется при изменении координат объекта.
4) Нелинейные системы и устройства зачастую используют в устройствах специального назначения, например, в различного типа генераторах периодических сигналов негармонического характера, (прямоугольных, треугольных, решетчатых и т.д.). Их синтез осуществляется из условия обеспечения соответствующего возбуждения (мягкого или жесткого), стабильности колебаний и т.д.
Рассмотрим кратко метод вибрационной линеаризации
U
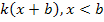
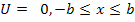
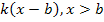
x
-b +b
Метод заключается в следующем.
К сигналу, поступающему на вход нелинейного звена с зоной нечувствительности добавляют гармонический сигнал, а после нелинейного звена ставят фильтр, удаляющий гармоническую составляющую с частотой.
| Asin(ωt) |
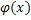 |
| φ |
| x |
| u |
| z |
| V(t) |
x, φ
x
u=x-b
+b
v
t1 t2 t3 t4 t
ψ1 ψ2 ψ3 ψ4 ψ
-b
Asin(ωt)
В качестве фильтра в простейшем случае применяют устройство со скользящим окном интегрирования:
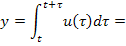
Поскольку в качестве интервала интегрирования взят период гармонического сигнала, то можно считать t=0.
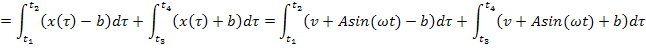
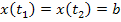
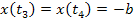
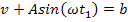
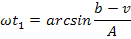
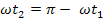
Интегрируя и суммируя интервалы, получим зависимость 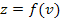 .
.
 2015-03-22
2015-03-22 755
755







