Если для точки покоя можно подобрать поверхность, охватывающую ее, такую, что все фазовые траектории проходят снаружи внутрь поверхности, то система будет асимптотически устойчива. Если же возможно, что фазовые траектории остаются на поверхности, то система будет устойчивая.
z
y
Если существует знакоопределенная функция  , производная от которой по времени
, производная от которой по времени 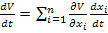 в силу дифференциальных уравнений системы
в силу дифференциальных уравнений системы 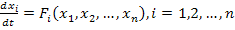 представляет собой также знакоопределенную функцию, противоположного с функцией
представляет собой также знакоопределенную функцию, противоположного с функцией 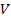 знака или равна 0, то невозмущенное движение будет устойчивым.
знака или равна 0, то невозмущенное движение будет устойчивым.
Если, кроме этого, значение производной от 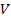 будет равно 0 в начале координат, то невозмущенное движение будет асимптотически устойчивым.
будет равно 0 в начале координат, то невозмущенное движение будет асимптотически устойчивым.
Для линейных систем функция 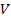 (функция Ляпунова) обычно определяется как квадратичная форма координат:
(функция Ляпунова) обычно определяется как квадратичная форма координат: 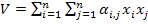 .
.
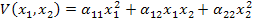
Проблема заключается в поиске такой функции.
Если она найдена и условие устойчивости выполняется, то система устойчива. Если она не существует, то система неустойчива. Но если она не найдена, это еще не значит, что она не существует.
Если система описывается уравнением
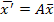 ,
,
где 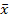 - вектор координат,
- вектор координат,
A – матрица координат.
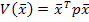 ,
, 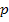 - положительно определенная матрица (все собственные числа положительные).
- положительно определенная матрица (все собственные числа положительные).
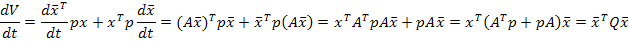
Если матрица 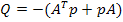 будет положительно определенной при положительно определенной матрице р, то замкнутая система будет устойчивой.
будет положительно определенной при положительно определенной матрице р, то замкнутая система будет устойчивой.
Поскольку матрица р не известна, то одновременно с оценкой и определением матрицы Q осуществляют поиск значений матрицы р, считают р и Q симметричными, причем собственные значения матрицы р должны быть положительными. Фактически производят подбор таких значений матрицы р, чтобы полученная матрица Q была положительно определенной.
Для нелинейных систем функцию Ляпунова зачастую определяют как квадратичную форму.
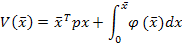
В инженерной практике абсолютно устойчивые нелинейные системы чаще исследуют с помощью критерия, предложенного румынским математиком В.М. Поповым.
| x |
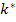
K* Если линейная система устойчива, т.е. ее характеристическое уравнение не содержит правых корней, а нелинейность принадлежит к классу К-функций, т.е. 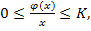 и можно подобрать такое вещественное число
и можно подобрать такое вещественное число 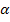 , что действительная часть функции
, что действительная часть функции
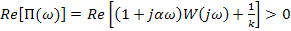 ,
,
где 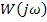 - частотная характеристика линейной части,
- частотная характеристика линейной части,
то замкнутая нелинейная система будет асимптотически устойчива.
Геометрическая формулировка критерия
Если к модифицированной частотной характеристике системы
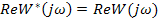
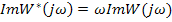 ,
,
можно провести прямую через точку 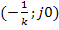 т.о., чтобы вся характеристика находилась справа от прямой, то при устойчивой линейной части замкнутая нелинейная система также будет устойчива.
т.о., чтобы вся характеристика находилась справа от прямой, то при устойчивой линейной части замкнутая нелинейная система также будет устойчива.
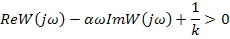
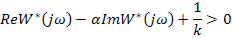
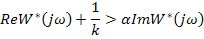
Прямая, проходящая через точку 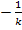 на оси абсцисс, может иметь следующее выражение:
на оси абсцисс, может иметь следующее выражение:
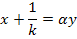
Im, y Кривая 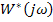 будет находиться справа от
будет находиться справа от
прямой, если при любых значениях
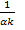
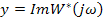 и
и 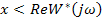 .
.
Re
x
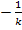
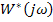
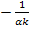
Перепишем последнее выражение:
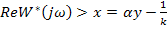
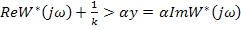 - условие устойчивости.
- условие устойчивости.
Система неустойчива система требует дополнительного исследования
Im
Im
Re 
 Re
Re
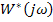
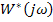
Если нелинейность разрывная, то 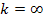 , тогда
, тогда 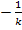 попадает в 0.
попадает в 0.
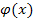
X
Если линейная часть неустойчива, т.е. характеристическое уравнение содержит правые корни,
а нелинейность можно описать зависимостью:
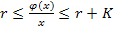 , причем
, причем 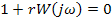 имеет все левые полюса (корни знаменателя), то замкнутая нелинейная система будет устойчива, если выполняется условие Попова для
имеет все левые полюса (корни знаменателя), то замкнутая нелинейная система будет устойчива, если выполняется условие Попова для
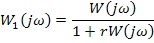
 2015-03-22
2015-03-22 1771
1771








