дифференцируемой в области  функции
функции  :
:
1) Найти все критические точки функции, принадлежащие  , и вычислить значения функции в них;
, и вычислить значения функции в них;
2) Найти наибольшее и наименьшее значения функции  на границах области;
на границах области;
3) Сравнить все найденные значения функции и выбрать из них наибольшее и наименьшее.
Пример. Найти наибольшее и наименьшее значение функции 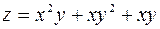 в замкнутой области, ограниченной линиями:
в замкнутой области, ограниченной линиями: 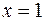 ,
, 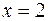 ,
, 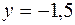 ,
, 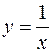 .
.
Решение. Здесь 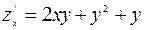 ,
, 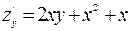 .
.
1) Находим все критические точки:
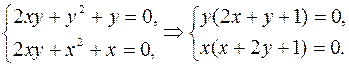
Решением системы являются точки 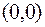 ,
, 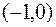 ,
,  ,
, 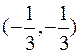 . Ни одна из найденных точек не принадлежит области
. Ни одна из найденных точек не принадлежит области  .
.
 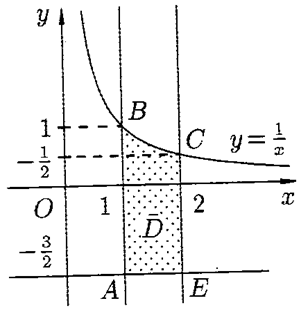 Рис. 12 Рис. 12 |
2) Исследуем функцию 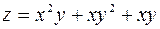 на границе области, состоящей из участков
на границе области, состоящей из участков 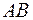 ,
, 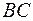 ,
, 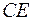 и
и 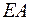 (см. рис. 12).
(см. рис. 12).
а)
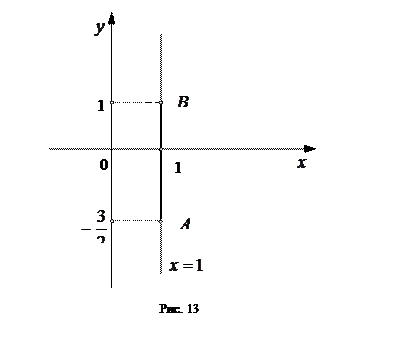
Участок 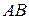 –отрезок вертикальной прямой
–отрезок вертикальной прямой 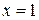 при
при 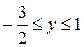 (см. рис. 13). При
(см. рис. 13). При 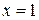 функция
функция 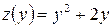 является функцией одного переменного
является функцией одного переменного 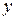 . Находим производную
. Находим производную 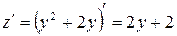 . Приравнивая ее к нулю
. Приравнивая ее к нулю 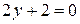 , находим стационарную точку
, находим стационарную точку 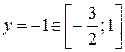 . Значение функции
. Значение функции 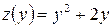 при
при 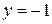 равно:
равно: 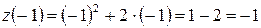 , а значение функции
, а значение функции 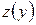 на концах отрезка
на концах отрезка 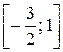 :
: 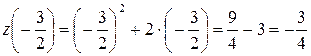 ,
,
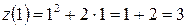 .
.
Следовательно, наименьшее значение функции 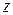 на отрезке
на отрезке 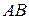 равно
равно 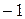 , а наибольшее
, а наибольшее 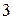 , то есть
, то есть 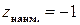 ,
, 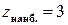 .
.
б)
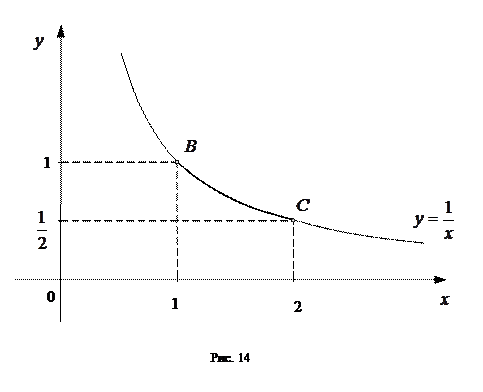
Участок 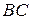 – дуга гиперболы
– дуга гиперболы 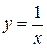 при
при 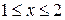 (см. рис. 14). При
(см. рис. 14). При 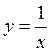 функция
функция 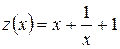 является функцией одного переменного
является функцией одного переменного 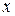 . Находим производную
. Находим производную 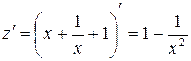 . Приравнивая ее к нулю
. Приравнивая ее к нулю 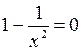 , находим
, находим 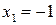 ,
, 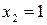 , из которых только одна точка
, из которых только одна точка 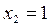 принадлежит отрезку
принадлежит отрезку 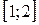 (см. рис. 14). Значение функции
(см. рис. 14). Значение функции 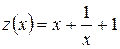 при
при 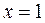 равно:
равно: 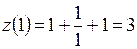 , а значение
, а значение 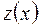 на правом конце отрезка
на правом конце отрезка 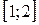 равно
равно 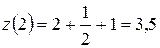 .
.
Следовательно, наименьшее значение функции 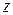 на участке
на участке 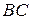 равно
равно 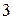 , а наибольшее
, а наибольшее 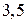 , то есть
, то есть 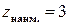 ,
, 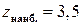 .
.
в)
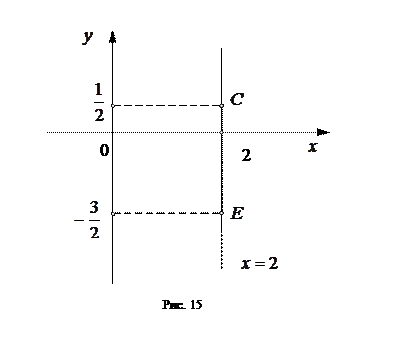
Участок 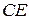 – отрезок вертикальной прямой
– отрезок вертикальной прямой 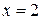 при
при 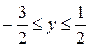 (см. рис. 15). При
(см. рис. 15). При 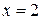 функция
функция 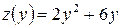 является функцией одного переменного
является функцией одного переменного 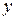 . Находим производную
. Находим производную 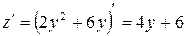 . Приравнивая ее к нулю:
. Приравнивая ее к нулю: 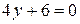 , находим точку
, находим точку 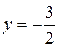 , совпадающую с левым концом отрезка
, совпадающую с левым концом отрезка 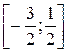 (см. рис. 15). Значение функции
(см. рис. 15). Значение функции 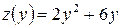 при
при 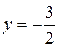 равно:
равно: 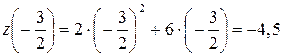 , а значение
, а значение 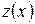 на правом конце отрезка
на правом конце отрезка 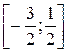 , то есть при
, то есть при 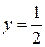 равно:
равно: 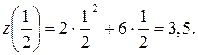
Следовательно, на отрезке 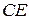 наименьшее значение равно
наименьшее значение равно 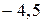 , а наибольшее
, а наибольшее 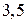 , то есть
, то есть 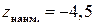 ,
, 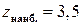 .
.
г)
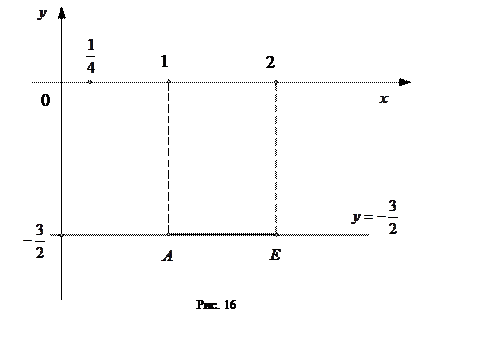
Участок 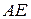 – отрезок горизонтальной прямой
– отрезок горизонтальной прямой  при
при  (см. рис.16). При
(см. рис.16). При 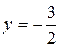 функция
функция 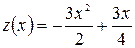 является функцией одного переменного
является функцией одного переменного 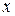 . Находим производную
. Находим производную 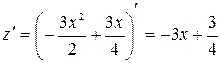 . Приравнивая ее к нулю:
. Приравнивая ее к нулю: 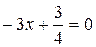 находим точку
находим точку 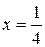 , которая не принадлежит отрезку
, которая не принадлежит отрезку 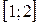 (см. рис. 16). Значения функции
(см. рис. 16). Значения функции 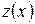 на концах отрезка
на концах отрезка 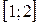 равны:
равны:
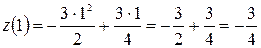 ;
;
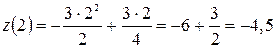 .
.
Следовательно, наименьшее значение 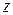 на отрезке
на отрезке 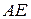 равно
равно 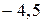 , а наибольшее
, а наибольшее 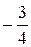 , то есть
, то есть 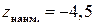 ,
, 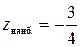 .
.
3) Сравнивая полученные результаты в пунктах а), б), в), г), имеем:
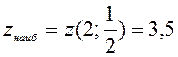
 .
.
Замечание. Площадь поперечного сечения канала называют его живым сечением, а длину Р границы такого сечения называют смоченным периметром канала. С помощью теоретических расчетов и эксперимента установлено [4], что из всех каналов с заданным живым сечением наибольшей пропускной способностью и одновременно наименьшей фильтрацией отличаются каналы с наименьшим смоченным периметром. Про такие каналы говорят, что они имеют гидравлически наивыгоднейший профиль.
Наиболее часто сооружают каналы, а также оросительные и водосточные канавы с сечением формы равнобочной трапеции (АВ=CD, см. рис. 17).
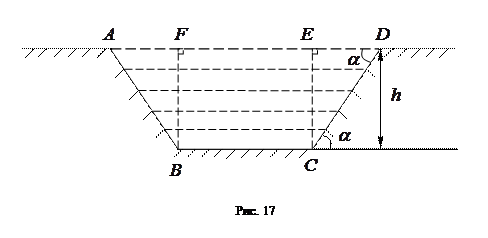
Пример. Найти наивыгоднейший с точки зрения гидравлики профиль канала трапецеидальной формы.
Решение. Найдем размеры поперечного сечения канала заданной площади S с наименьшим периметром 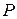 . Пусть
. Пусть 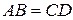 ,
, 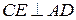 ,
, 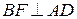 ,
, 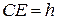 ,
, 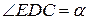 . Тогда
. Тогда
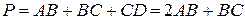 (1)
(1)
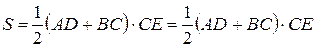 (2)
(2)
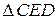 – прямоугольный
– прямоугольный
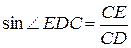 или
или 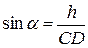 , откуда
, откуда
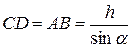 (3)
(3)
Подставив (3) в (1), получаем:
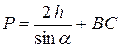 (4)
(4)
Так как 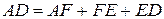 , а
, а 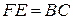 ,
, 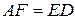 , находим:
, находим:
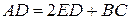 (5)
(5)
Из 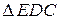 :
: 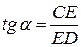 или
или 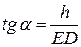 , откуда
, откуда 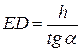 . Подставив последнее равенство в (5), находим
. Подставив последнее равенство в (5), находим 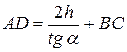 . Тогда равенство (2) запишется:
. Тогда равенство (2) запишется: 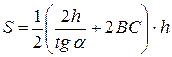 , откуда
, откуда 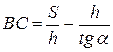 . Подставив последнее равенство в (3), находим
. Подставив последнее равенство в (3), находим 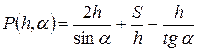 .
.
Таким образом, требуется найти такую точку 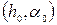 из области
из области 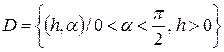 , в которой функция
, в которой функция 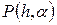 принимает наименьшее значение.
принимает наименьшее значение.
Найдя частные производные функции 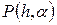 и приравняв их к нулю, получим систему уравнений:
и приравняв их к нулю, получим систему уравнений:
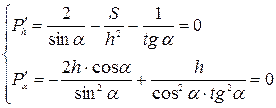
или
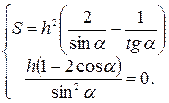
Откуда 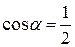 или
или 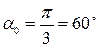 , тогда
, тогда 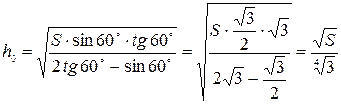 .
.
В рассматриваемой области 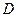 функция
функция 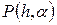 имеет единственную критическую точку
имеет единственную критическую точку 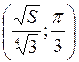 , значение функции в ней равно P=
, значение функции в ней равно P= 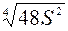 .
.
Исследуем функцию 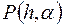 на границе области
на границе области 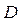 :
:
1) 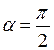 ,
, 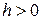 . Имеем
. Имеем 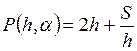
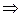
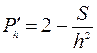
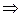
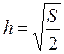 . Тогда
. Тогда
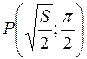 =
= 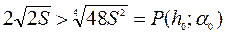 .
.
2) При приближении точки 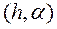 к прямым
к прямым 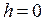 и
и 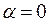 , а также при удалении в бесконечность по
, а также при удалении в бесконечность по 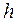 функция
функция 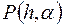 неограниченно возрастает. Поэтому точку
неограниченно возрастает. Поэтому точку 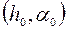 можно окружить таким прямоугольником
можно окружить таким прямоугольником 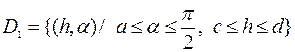 , что вне его и на его границе
, что вне его и на его границе 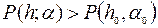 .
.
Отсюда следует, что 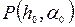 – наименьшее значение функции
– наименьшее значение функции 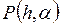 в области
в области 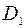 , и оно же будет наименьшим значением этой функции в области
, и оно же будет наименьшим значением этой функции в области  .
.
Итак, функция 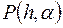 имеет наименьшее значение при
имеет наименьшее значение при 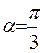 ,
, 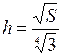 .
.
Таким образом в трапеции 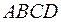 :
: 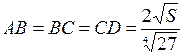 и
и 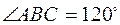 .
.
 2015-03-22
2015-03-22 1371
1371
