Свойства определенного интеграла вытекают из основных свойств сумм и пределов.
1. Постоянный сомножитель можно вынести за знак определенного интеграла:
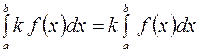 ,
, 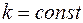 .
.
2. Определенный интеграл от алгебраической суммы двух функций 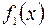 и
и 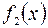 , интегрируемых на
, интегрируемых на 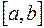 , равен алгебраической сумме определенных интегралов от этих функций, т.е.
, равен алгебраической сумме определенных интегралов от этих функций, т.е.
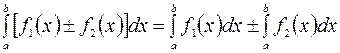 .
.
Данное свойство распространяется и на сумму любого конечного числа интегрируемых функций.
3. Если отрезок интегрирования 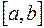 разбит точкой
разбит точкой 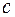 на два отрезка
на два отрезка 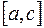 и
и 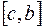 , то интеграл по всему отрезку равен сумме интегралов по его частям:
, то интеграл по всему отрезку равен сумме интегралов по его частям:
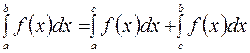 .
.
Точка 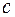 может находиться и вне отрезка
может находиться и вне отрезка 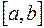 .
.
4. Интеграл с равными пределами интегрирования 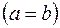 равен нулю, т.е.
равен нулю, т.е.
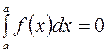 .
.
5. Если в определенном интеграле поменять местами пределы интегрирования, то знак интеграла изменится на противоположный:
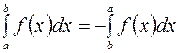 .
.
6. Теорема о среднем значении.
Если 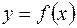 непрерывна на
непрерывна на 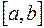 , то существует такая точка
, то существует такая точка 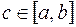 , что справедливо следующее равенство:
, что справедливо следующее равенство:
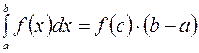 .
.
Нетрудно понять геометрический смысл этого равенства: интеграл, стоящий слева есть площадь криволинейной трапеции. Произведение, стоящее в правой части равенства, - площадь равновеликого ей прямоугольника с высотой 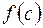 и основанием
и основанием 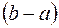 (см. рис. 20).
(см. рис. 20).
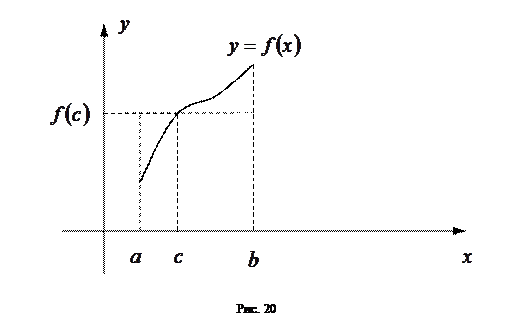
Число 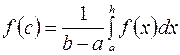 называется средним значением функции
называется средним значением функции 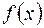 на отрезке
на отрезке 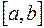 .
.
7. Производная от определенного интеграла по переменному верхнему пределу равна подынтегральной функции, взятой при значении верхнего предела:
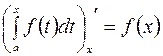 .
.
 2015-03-22
2015-03-22 747
747








