2015-03-22
1581
Допустим, что некоторая сила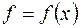 
, направленная вдоль оси 
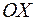, на отрезке 
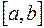совершает работу (см. рис. 19). Если 
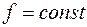, то работа 
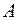вычисляется по формуле 
.
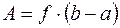Определим работу 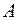переменной силы 
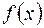на отрезке :
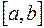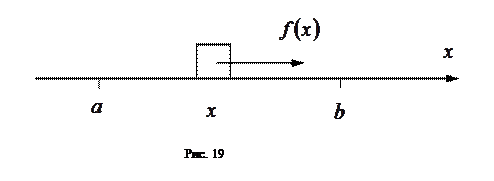
Для этого: разобьем отрезок 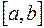с помощью произвольно расположенных, следующих друг за другом точек 
, 
, 
,..., 
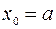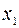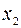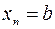. Это разбиение производим достаточно мелко, так, чтобы на интервалах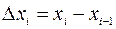 
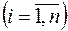величина 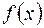практически не изменялась. Пусть она равняется 
, 
, 
(
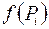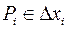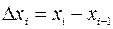
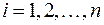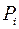– произвольно выбранные точки). Величина работы силы 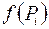на участке 
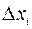вычисляется по формуле: 
;
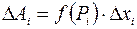Определение. Предел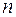 
-ой интегральной суммы для функции 
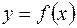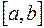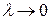
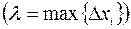на отрезке при 
и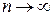 
называется определенным интегралом от функции 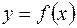в пределах от 
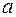до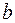 
(обозначение 
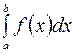), т.е.:
,
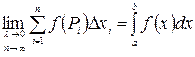где 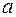– нижний предел интегрирования,
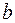– верхний предел интегрирования,
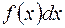– подынтегральное выражение,
Геометрический смысл определенного интеграла – площадь криволинейной трапеции.
Физический смысл определенного интеграла. Здесь его возможности очень широки. В частности, можно определить массу стержня, работу силы на заданном отрезке пути и т.д.
