Три единичных взаимно перпендикулярных вектора 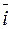 ,
, 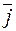 ,
, 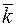 пространства, через которые условились выражать все векторы пространства, называются базисными векторами или базисом.
пространства, через которые условились выражать все векторы пространства, называются базисными векторами или базисом.
Прямоугольной декартовой системой координат в пространстве называется совокупность точки 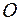 и базиса
и базиса 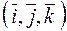 . (См. рис. 6)
. (См. рис. 6)
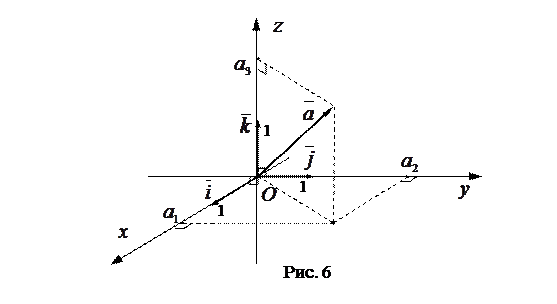
Точка  называется началом координат, оси
называется началом координат, оси  ,
, 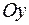 и
и 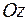 , проходящие через начало координат – точку
, проходящие через начало координат – точку 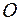 в направлении базисных векторов
в направлении базисных векторов 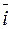 ,
, 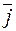 и
и 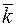 называются осями координат. Плоскости
называются осями координат. Плоскости 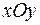 ,
, 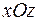 и
и 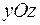 , проходящие через каждую пару осей координат называются координатными плоскостями.
, проходящие через каждую пару осей координат называются координатными плоскостями.
Если выбрана прямоугольная декартова система координат, то любой вектор  пространства может быть единственным образом разложен по векторам
пространства может быть единственным образом разложен по векторам 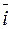 ,
, 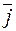 ,
, 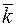 базисным как:
базисным как:
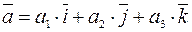 ,
,
то есть для каждого вектора  пространства в выбранной прямоугольной декартовой системе координат найдется единственная тройка чисел – координат
пространства в выбранной прямоугольной декартовой системе координат найдется единственная тройка чисел – координат 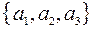 , что позволяет написать равенство:
, что позволяет написать равенство: 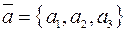 (см. рис. 6).
(см. рис. 6).
Если два вектора  и
и  в прямоугольной декартовой системе координат заданы своими координатами, то есть
в прямоугольной декартовой системе координат заданы своими координатами, то есть 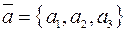 ,
, 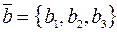 , то
, то
1) 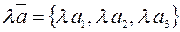 ;
;
2) 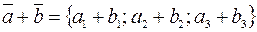 .
.
Пример. Найти координаты вектора 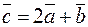 , если
, если 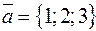 ,
, 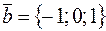 .
.
Решение:
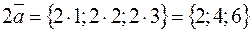 .
.
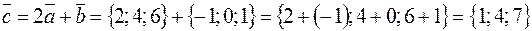 .
.
Ответ: 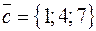 .
.
Для произвольной точки 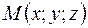 в прямоугольной декартовой системе координат координатами вектора
в прямоугольной декартовой системе координат координатами вектора 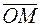 являются проекции вектора на оси
являются проекции вектора на оси 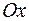 ,
, 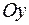 ,
, 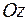 соответственно, то есть
соответственно, то есть 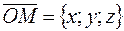 . (См. рис. 7)
. (См. рис. 7)
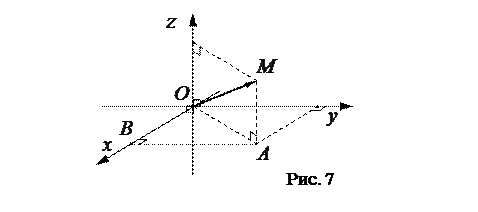
Длина вектора 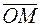 находится из двух прямоугольных треугольников
находится из двух прямоугольных треугольников 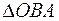 и
и 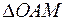 :
:
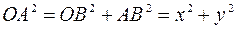 ;
;
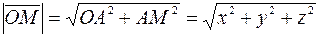 .
.
Пример. Найти 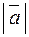 , если
, если 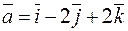 .
.
 2015-03-22
2015-03-22 4419
4419








