Линейными операциями над векторами называются сложение векторов и умножение вектора на число.
Суммой двух векторов  и
и  называется третий вектор
называется третий вектор 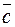 , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора  , а конец – с концом вектора
, а конец – с концом вектора  , при чем конец вектора
, при чем конец вектора  и начало вектора
и начало вектора  совмещаются и обозначается:
совмещаются и обозначается: 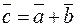 .
.
Пусть даны вектора  и
и  . (См. рис. 2)
. (См. рис. 2)
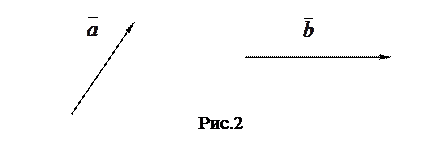
Чтобы их сложить, то есть найти сумму 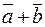 этих векторов, необходимо нарисовать
этих векторов, необходимо нарисовать  и
и  в одном и том же масштабе таким образом, чтобы начало вектора
в одном и том же масштабе таким образом, чтобы начало вектора  – второго слагаемого, совпало с концом вектора
– второго слагаемого, совпало с концом вектора  – первого слагаемого (см. рис. 3). Тогда отрезок, соединяющий начало вектора
– первого слагаемого (см. рис. 3). Тогда отрезок, соединяющий начало вектора  с концом вектора
с концом вектора  будет суммой
будет суммой 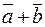 в том же масштабе, в котором представлены
в том же масштабе, в котором представлены  и
и  .
.
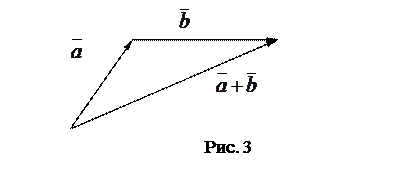
Противоположным вектору  называется такой вектор
называется такой вектор 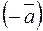 , который при сложении с вектором
, который при сложении с вектором  дает нуль-вектор, то есть
дает нуль-вектор, то есть 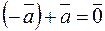 .
.
Заметим, что разностью векторов  и
и  является сумма вектора
является сумма вектора  и вектора
и вектора 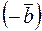 , противоположного вектору
, противоположного вектору  , то есть
, то есть 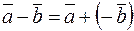 .
.
Произведением вектора  на число
на число 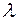 называется такой вектор
называется такой вектор 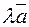 , направление которого совпадает с вектором
, направление которого совпадает с вектором  , если
, если 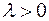 и противоположно направлению вектора
и противоположно направлению вектора  , если
, если 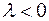 ; длина же вектора
; длина же вектора 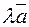 в
в 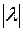 раз «больше» длины вектора
раз «больше» длины вектора  , то есть
, то есть
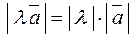 .
.
Пусть дан вектор  (см. рис. 4), тогда векторы
(см. рис. 4), тогда векторы 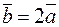 ,
, 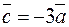 изображены на рисунке 5.
изображены на рисунке 5.
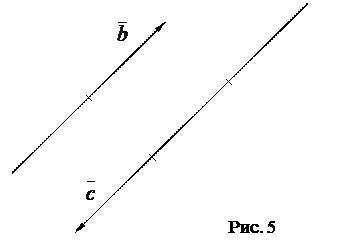
Свойства линейных операций над векторами:
1. 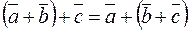
2. 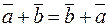
3. 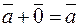
4. 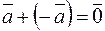
5. 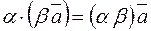
6. 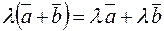
7. 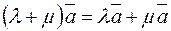
8. 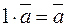 , где
, где 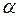 ,
, 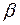 ,
, 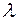 ,
, 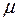 – действительные числа.
– действительные числа.
 2015-03-22
2015-03-22 541
541








