Три некомпланарных (непараллельных одной плоскости) вектора  ,
,  и
и 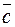 , взятые в указанном порядке, образуют правую тройку векторов, если из конца третьего вектора
, взятые в указанном порядке, образуют правую тройку векторов, если из конца третьего вектора 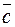 поворот от первого вектора
поворот от первого вектора  ко второму вектору
ко второму вектору  по кротчайшему пути виден против хода часовой стрелки, и левую, если по часовой. (См. рис. 8)
по кротчайшему пути виден против хода часовой стрелки, и левую, если по часовой. (См. рис. 8)

Векторным произведением вектора  на вектор
на вектор  называется такой вектор
называется такой вектор 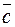 , что:
, что:
1)  ,
, 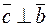 ;
;
2) 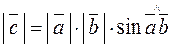 ;
;
3) тройка векторов  ,
,  , и
, и 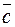 – правая, и обозначается
– правая, и обозначается 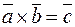 .
.
Из определения векторного произведения непосредственно вытекают следующие соотношения между ортами 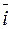 ,
, 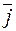 , и
, и 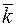 :
:
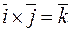 ,
, 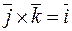 ,
, 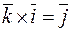 .
.
Поскольку тройки векторов 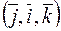 ,
, 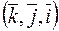 и
и 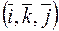 левые, то
левые, то
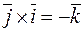 ,
, 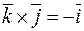 ,
, 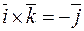 .
.
Свойства векторного произведения:
1) 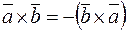 ;
;
2) 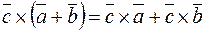 ;
;
3) 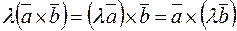 ,
, 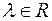 ;
;
4) 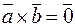
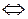
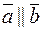 .
.
Векторное произведение двух векторов 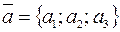 и
и 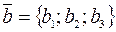 находится по формуле:
находится по формуле:
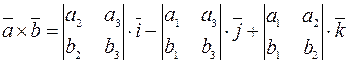 .
.
Пример. Найти векторное произведение векторов 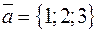 и
и 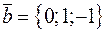 .
.
 2015-03-22
2015-03-22 685
685








