Скалярным произведением двух ненулевых векторов  и
и  называется число, равное произведению длин векторов на косинус угла между ними и обозначается:
называется число, равное произведению длин векторов на косинус угла между ними и обозначается: 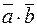 , то есть
, то есть
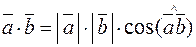 .
.
Свойства скалярного произведения:
1) 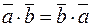 ;
;
2) 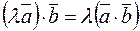 ,
, 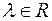 ;
;
3) 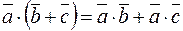 ;
;
4) 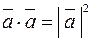 или
или
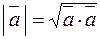 . (2.1)
. (2.1)
Пример. Найти длину вектора 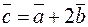 , если
, если 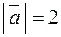 ,
, 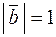 ,
, 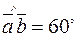 .
.
Решение. По формуле (2.1), находим
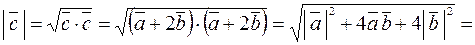
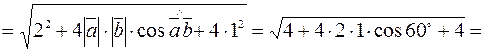
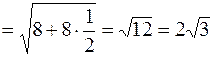 .
.
Ответ: 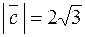 .
.
Если два вектора  и
и  заданы своими координатами:
заданы своими координатами: 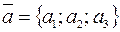 и
и 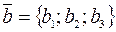 , то их скалярное произведение находим по формуле:
, то их скалярное произведение находим по формуле:
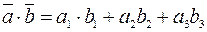 . (2.2)
. (2.2)
Пример. Найти скалярное произведение векторов 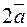 и
и 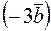 , если
, если 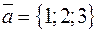 и
и 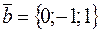 .
.
Решение. Координаты векторов 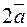 и
и 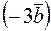 :
:
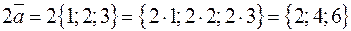 ;
;
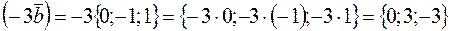 .
.
По формуле (2.2) искомое скалярное произведение равно:
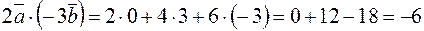 .
.
Ответ: 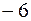 .
.
Некоторые приложения скалярного произведения:
1. Угол между двумя ненулевыми векторами 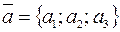 и
и 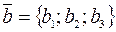 из определения скалярного произведения вычисляется по формуле:
из определения скалярного произведения вычисляется по формуле:
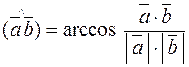 или
или
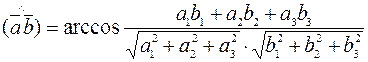 (2.3)
(2.3)
Пример. Найти угол между векторами 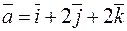 и
и 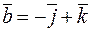 .
.
Решение. Координаты векторов  и
и  :
: 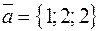 и
и 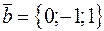 .
.
Тогда по формуле (2.3), угол между векторами  и
и  равен:
равен:
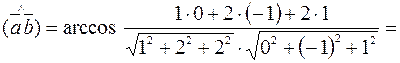
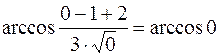 , следовательно,
, следовательно, 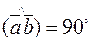 , то есть
, то есть 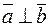 .
.
Ответ: 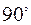 .
.
2. Проекция вектора  на вектор
на вектор  вычисляется по формуле:
вычисляется по формуле:
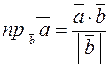 .
.
Пример. Найти 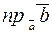 , если
, если 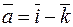 и
и 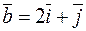 .
.
Решение. Координаты векторов 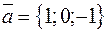 ,
, 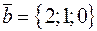 . Тогда
. Тогда
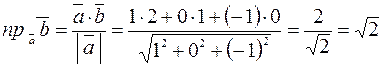 .
.
Ответ: 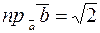 .
.
 2015-03-22
2015-03-22 750
750








