Пределом функции  в точке
в точке 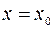 называется такое число
называется такое число 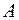 , что для любой последовательности
, что для любой последовательности 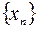 значений аргумента
значений аргумента 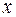 , сходящейся к числу
, сходящейся к числу  , последовательность
, последовательность 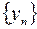 ,
, 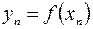 соответствующих значений функции
соответствующих значений функции  стремится к этому числу
стремится к этому числу 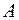 и обозначается:
и обозначается: 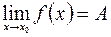 .
.
При нахождении пределов функций нужно использовать следующие свойства предела функции: если существуют конечные пределы 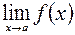 и
и 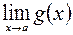 , то
, то
1) 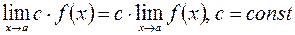 ;
;
2) 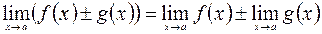 ;
;
3) 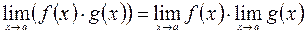 ;
;
4) 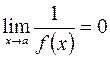 (или
(или 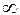 ), если
), если 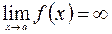 (или 0);
(или 0);
5) 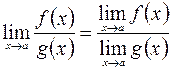 , если
, если 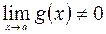 .
.
Пример. Вычислить 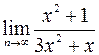 .
.
Решение: Разделим числитель и знаменатель на 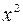 , получим:
, получим:
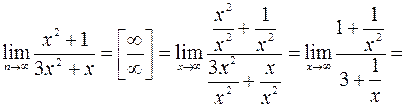
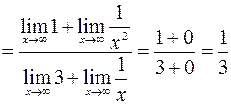 .
.
При нахождении пределов функций также полезно знать первый замечательный предел: 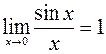 и следствия из него:
и следствия из него:
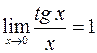 ;
; 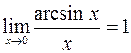 ;
; 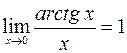 ;
;
и второй замечательный предел: 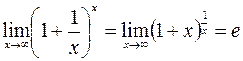 .
.
Пример. Вычислить предел 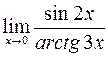 .
.
 2015-03-22
2015-03-22 350
350








