Пусть функция 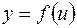 определена на множестве
определена на множестве 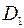 , а функция
, а функция 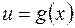 определена на множестве
определена на множестве 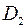 , причем для любой точки
, причем для любой точки 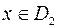 , соответствует значение
, соответствует значение 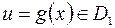 . Тогда на множестве
. Тогда на множестве 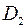 определена функция
определена функция 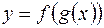 , которая называется сложной функцией от
, которая называется сложной функцией от 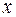 (или функцией от функции).
(или функцией от функции).
Переменную 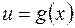 называют промежуточным аргументом сложной функции
называют промежуточным аргументом сложной функции  .
.
Пример. Функция 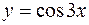 является сложной функцией, так как
является сложной функцией, так как 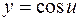 ,
, 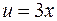 .
.
Пусть 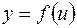 ,
, 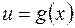 , тогда
, тогда 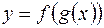 – сложная функция с промежуточным аргументом
– сложная функция с промежуточным аргументом 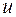 и независимым аргументом
и независимым аргументом 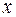 . Тогда производная сложной функции
. Тогда производная сложной функции  по независимой переменной
по независимой переменной 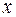 равна произведению производной функции
равна произведению производной функции  по промежуточной переменной
по промежуточной переменной 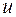 на производную промежуточной переменной
на производную промежуточной переменной 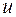 по независимой переменной
по независимой переменной 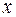 , то есть
, то есть 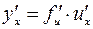 .
.
Пример. Найти производную функции 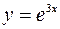 .
.
Решение. Данная функция  является сложной, так как
является сложной, так как 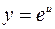 ,
, 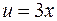 . По правилу дифференцирования сложной функции, находим:
. По правилу дифференцирования сложной функции, находим:
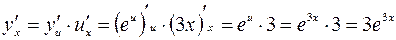 .
.
 2015-03-22
2015-03-22 323
323








