Пусть функция  определена на некотором интервале
определена на некотором интервале 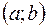 . Аргументу
. Аргументу 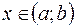 дадим приращение
дадим приращение 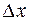 , получим точку
, получим точку 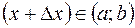 . Найдем соответствующее приращение функции:
. Найдем соответствующее приращение функции: 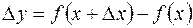 . Составим отношение приращения
. Составим отношение приращения 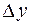 функции
функции  к приращению
к приращению 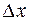 аргумента
аргумента 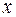 :
: 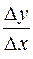 и найдем предел этого отношения при
и найдем предел этого отношения при 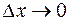 , то есть
, то есть 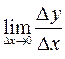 . Если этот предел существует, то его называют производной функцией от данной функции
. Если этот предел существует, то его называют производной функцией от данной функции  и обозначают одним из символов:
и обозначают одним из символов: 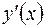 ,
, 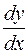 ,
, 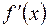 ,
, 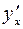 .
.
Итак, по определению
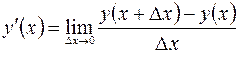 .
.
Функция  , имеющая производную в каждой точке интервала
, имеющая производную в каждой точке интервала 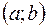 , называется дифференцируемой в этом интервале, а операция нахождения производной функции называется дифференцированием.
, называется дифференцируемой в этом интервале, а операция нахождения производной функции называется дифференцированием.
Значения производной функции  в точке
в точке 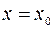 обозначается одним из символов:
обозначается одним из символов: 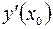 ,
, 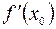 или
или 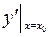 .
.
Пример. Найти по определению производную функции 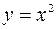 .
.
Решение. Областью определения  данной функции является вся числовая ось, то есть
данной функции является вся числовая ось, то есть 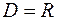 . Выберем произвольную точку
. Выберем произвольную точку 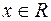 . Дадим ей приращение
. Дадим ей приращение 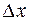 , получим новую точку
, получим новую точку 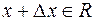 . Находим соответствующее приращение
. Находим соответствующее приращение 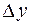 функции
функции 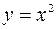 :
:
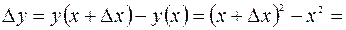
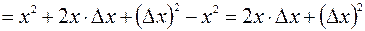 .
.
Составим отношение 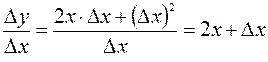 и найдем предел отношения при
и найдем предел отношения при 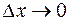 :
:
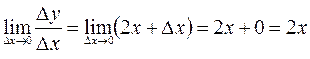 .
.
Поскольку данный предел существует, то производная функции 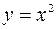 в точке
в точке 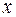 равна
равна 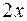 , то есть
, то есть 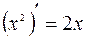 .
.
Пусть материальная точка (тело) движется неравномерно по закону прямолинейного движения 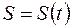 . Каждому значению истекшего времени
. Каждому значению истекшего времени 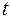 соответствует определенное расстояние
соответствует определенное расстояние 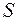 до некоторой фиксированной точки
до некоторой фиксированной точки 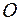 . Тогда средняя скорость
. Тогда средняя скорость 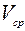 движения точки за время
движения точки за время 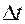 равна:
равна:
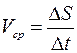 , где
, где 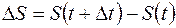 .
.
Предел средней скорости 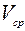 движения при стремлении к нулю промежутка времени
движения при стремлении к нулю промежутка времени 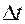 называется скоростью
называется скоростью 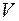 движения точки в данный момент времени (или мгновенной скоростью)
движения точки в данный момент времени (или мгновенной скоростью)
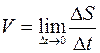 .
.
Таким образом, скорость прямолинейного движения материальной точки в момент времени 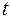 есть производная от пути
есть производная от пути 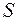 по времени
по времени 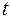 , то есть
, то есть 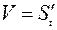 . В этом заключается механический смысл производной.
. В этом заключается механический смысл производной.
Если функция  описывает какой-либо физический процесс, то производная
описывает какой-либо физический процесс, то производная 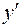 есть скорость протекания этого процесса. В этом состоит физический смысл производной.
есть скорость протекания этого процесса. В этом состоит физический смысл производной.
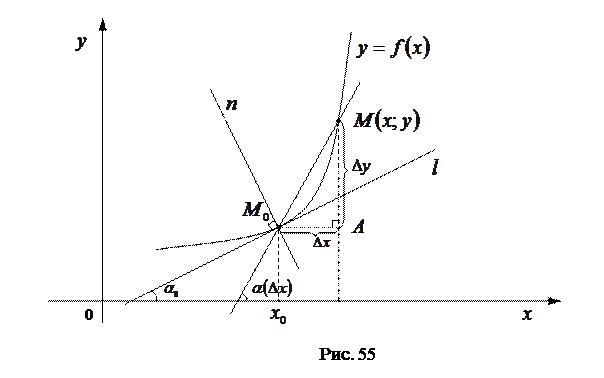 Под касательной
Под касательной 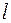 к графику функции
к графику функции  в точке
в точке 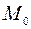 понимают предельное положение секущей
понимают предельное положение секущей 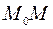 , когда точка
, когда точка 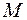 движется по кривой к точке
движется по кривой к точке 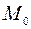 (см. рис. 55). Нормалью
(см. рис. 55). Нормалью 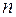 называется прямая, проходящая через данную точку
называется прямая, проходящая через данную точку 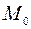 перпендикулярно касательной
перпендикулярно касательной 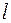 (см. рис. 55).
(см. рис. 55).
Пусть касательная 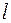 образует с положительным направлением оси
образует с положительным направлением оси 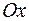 угол
угол 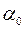 , а секущая
, а секущая 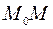 – угол
– угол 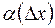 . Тогда из прямоугольного треугольника
. Тогда из прямоугольного треугольника 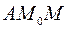 , получаем:
, получаем: 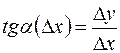 . Переходя к пределу при
. Переходя к пределу при 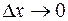 , находим:
, находим:
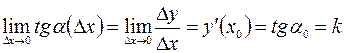 ,
,
То есть производная 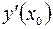 в точке
в точке  равна угловому коэффициенту
равна угловому коэффициенту 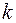 касательной
касательной 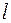 к графику функции
к графику функции  в точке, абсцисса которой равна
в точке, абсцисса которой равна  . В этом заключается геометрический смысл производной.
. В этом заключается геометрический смысл производной.
Пользуясь уравнением прямой, проходящей через заданную точку 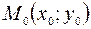 в заданном направлении
в заданном направлении 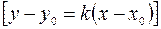 , запишем уравнение касательной
, запишем уравнение касательной 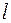 к графику функции
к графику функции  в точке
в точке 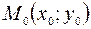 :
:
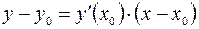 .
.
Поскольку нормаль 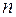 перпендикулярна касательной
перпендикулярна касательной 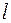 , то ее угловой коэффициент
, то ее угловой коэффициент 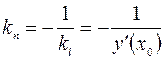 . Поэтому уравнение нормали
. Поэтому уравнение нормали 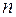 к кривой
к кривой  в точке
в точке 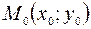 имеет вид:
имеет вид:
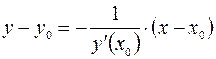 .
.
Пример. Составить уравнение касательной и нормали к кривой 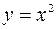 в точке
в точке  .
.
Решение. Поскольку 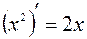 , то
, то
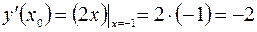
и искомое уравнение касательной:
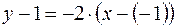 или
или 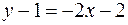 ,
,
откуда 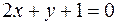 , а искомое уравнение нормали:
, а искомое уравнение нормали:
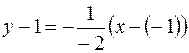 или
или 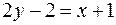 ,
,
откуда
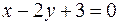 .
.
Нахождение производной функции непосредственно по определению часто связано с некоторыми трудностями. На практике функции дифференцируют с помощью правил и формул.
Запишем формулы производных элементарных функций:
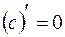 ,
, 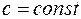 ;
; 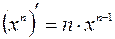 ,
, 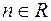 ,
, 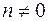 ;
;
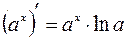 ,
, 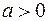 ,
,  ;
; 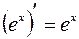 ;
;
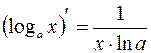 ,
, 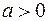 ,
,  ;
; 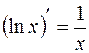 ;
;
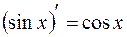 ;
; 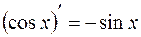 ;
;
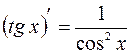 ;
; 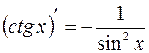 ;
;
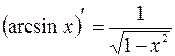 ;
; 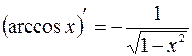 ;
;
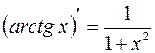 ;
; 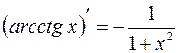 ;
;
а также формулы, выражающие правила дифференцирования:
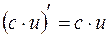 ,
, 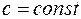 ,
, 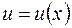 ;
;
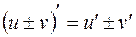 ,
, 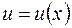 ,
, 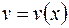 ;
;
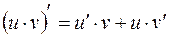 ,
, 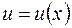 ,
, 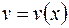 ;
;
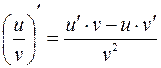 ,
, 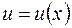 ,
, 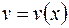 .
.
Пример. Найти производную функции 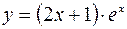 .
.
Решение. По правилу дифференцирования произведения двух функций, находим:
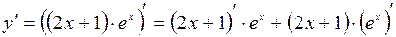 .
.
Далее, по правилу дифференцирования суммы двух функций и произведения числа на функцию и формул производных степеней и показательной функций, находим:
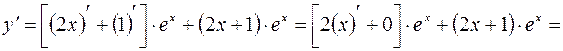
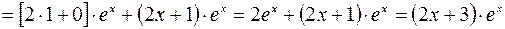 .
.
 2015-03-22
2015-03-22 466
466








