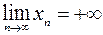 означает, что
означает, что 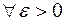
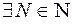 ,
, 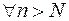
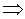
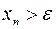 ;
;
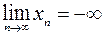 означает, что
означает, что 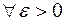
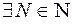 ,
, 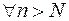
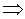
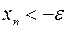 .
.
При вычислении пределов числовой последовательности полезно использовать следующие их свойства, если существуют конечные пределы 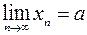 и
и 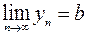 , то
, то
1) 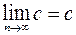 ,
, 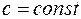 ;
;
2) 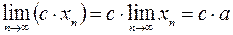 ,
, 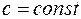 ;
;
3) 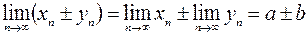 ;
;
4) 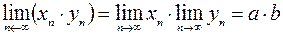 ;
;
5) 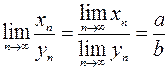 , если
, если 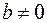 ;
;
6) 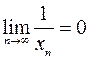 , если
, если 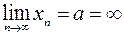 .
.
Пусть требуется найти предел 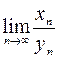 отношения двух последовательностей, сходящихся к бесконечности, то есть
отношения двух последовательностей, сходящихся к бесконечности, то есть 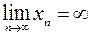 и
и 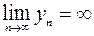 .
.
Непосредственно применить свойство о пределе частного двух последовательностей нельзя. Предварительно необходимо преобразовать выражение 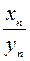 к виду, допускающему применение указанных свойств. В связи с этим выражение
к виду, допускающему применение указанных свойств. В связи с этим выражение 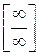 называется неопределенностью, а его преобразование к виду, позволяющему найти предел – раскрытие неопределенности.
называется неопределенностью, а его преобразование к виду, позволяющему найти предел – раскрытие неопределенности.
Заметим, что выражение 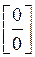 , когда последовательности в числителе и знаменателе стремятся к нулю, также называются неопределенностью.
, когда последовательности в числителе и знаменателе стремятся к нулю, также называются неопределенностью.
Пример. Вычислить 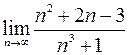 .
.
Решение. Разделим числитель и знаменатель на 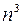 – наибольшую из степеней
– наибольшую из степеней 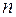 в числителе и знаменателе:
в числителе и знаменателе:
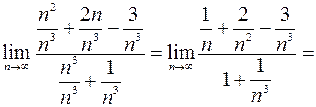
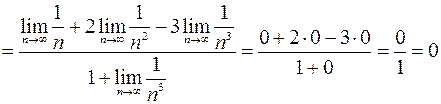 .
.
 2015-03-22
2015-03-22 229
229








