Функция 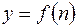 , заданная на множестве
, заданная на множестве 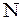 всех натуральных чисел
всех натуральных чисел 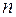 называется числовой последовательностью и обозначается
называется числовой последовательностью и обозначается 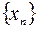 , где элемент
, где элемент 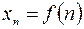 соответствует номеру
соответствует номеру 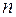 . Будем задавать числовую последовательность
. Будем задавать числовую последовательность 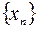 формулой своего общего члена
формулой своего общего члена 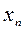 .
.
Пример. 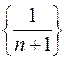 – числовая последовательность
– числовая последовательность 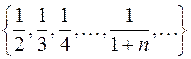 , так как
, так как 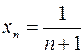 – формула общего члена последовательности.
– формула общего члена последовательности.
При 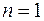 :
: 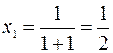 .
.
При 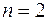 :
: 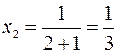 .
.
При 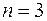 :
: 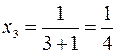 и т.д.
и т.д.
Пределом числовой последовательности 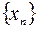 называется конечное действительное число
называется конечное действительное число 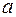 , если для любого сколь угодно малого числа
, если для любого сколь угодно малого числа 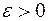 существует такое натуральное число
существует такое натуральное число 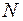 , что для всех членов последовательности с номерами
, что для всех членов последовательности с номерами 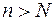 выполняется неравенство
выполняется неравенство 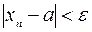 . В краткой записи это выглядит так:
. В краткой записи это выглядит так:
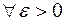
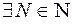
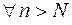
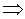
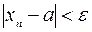
и обозначается: 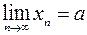 .
.
Определим 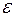 – окрестность точки
– окрестность точки 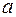 как множество всех
как множество всех 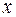 , удовлетворяющих условию:
, удовлетворяющих условию: 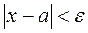 , что эквивалентно двойному неравенству:
, что эквивалентно двойному неравенству: 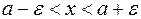 .
.
Тогда понятие предела геометрически означает, что какую бы малую 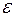 – окрестность точки
– окрестность точки 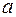 не взяли, найдется такой номер
не взяли, найдется такой номер 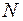 , начиная с которого все последующие члены последовательности будут находиться в этой окрестности (См. рис. 52).
, начиная с которого все последующие члены последовательности будут находиться в этой окрестности (См. рис. 52).
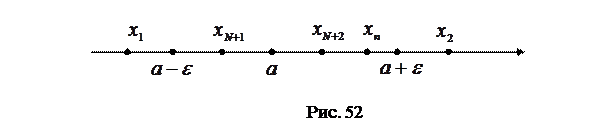
Последовательность, имеющая конечный предел, называется сходящейся или стремящейся к этому пределу, а неимеющая конечного предела – расходящейся. «Стремление» последовательности 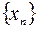 к своему пределу
к своему пределу 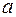 будем обозначать как
будем обозначать как 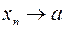 .
.
Пример. Доказать по определению, что 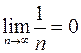 .
.
Решение. Возьмем любое сколь угодно малое 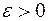 . Имеем:
. Имеем: 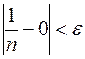 , когда
, когда 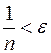 или
или 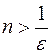 . Значит существует такой номер
. Значит существует такой номер 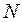 , равный целой части числа
, равный целой части числа 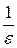 , то есть такое целое число
, то есть такое целое число 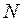 , что
, что 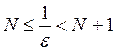 , то есть
, то есть 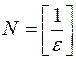 , начиная с которого все последующие члены с номерами
, начиная с которого все последующие члены с номерами 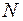 ,
, 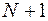 ,
, 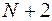 ,
, 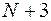 ,... будут находиться в
,... будут находиться в 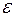 – окрестности точки
– окрестности точки 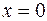 , то есть в интервале
, то есть в интервале 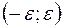 . (См. рис.53). При
. (См. рис.53). При 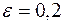
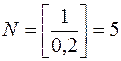 , при
, при 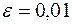
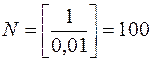 .
.
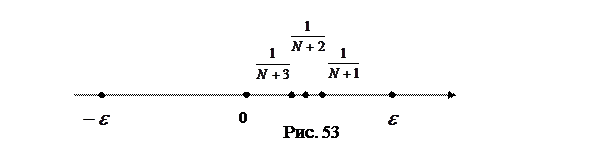
 2015-03-22
2015-03-22 299
299








