Прямую 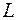 называют асимптотой графика функции
называют асимптотой графика функции  , если расстояние до точки
, если расстояние до точки 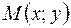 кривой
кривой  от прямой
от прямой 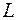 стремится к нулю при неограниченном удалении этой точки по кривой от начала координат.
стремится к нулю при неограниченном удалении этой точки по кривой от начала координат.
Прямая 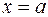 является вертикальной асимптотой кривой
является вертикальной асимптотой кривой  , если
, если 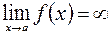 .
.
Прямая 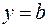 является горизонтальной асимптотой кривой
является горизонтальной асимптотой кривой  , если
, если 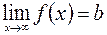 .
.
Прямая 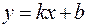 является наклонной асимптотой кривой
является наклонной асимптотой кривой  , если существуют пределы:
, если существуют пределы:
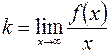 и
и 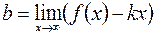 .
.
Пример. Найти асимптоты кривой 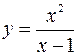 .
.
Решение. Данная функция определена в интервалах 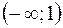 и
и 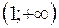 .
.
Так как 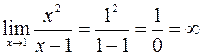 , то прямая
, то прямая 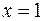 есть вертикальная асимптота данной кривой.
есть вертикальная асимптота данной кривой.
Горизонтальных асимптот кривая не имеет, так как предел 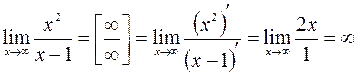 не является конечной величиной.
не является конечной величиной.
Наклонные асимптоты находим в виде уравнения прямой 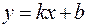 :
:
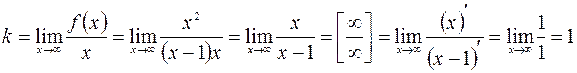 ;
;
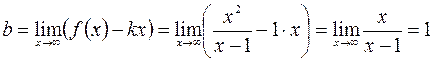 .
.
Таким образом, существует наклонная асимптота 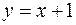 .
.
 2015-03-22
2015-03-22 1036
1036








