Функция  называется четной, если
называется четной, если 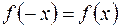 . График четной функции симметричен относительно оси
. График четной функции симметричен относительно оси 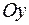 .
.
Пример. Функция 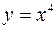 является четной, так как,
является четной, так как, 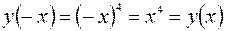 , следовательно, график этой функции симметричен относительно оси
, следовательно, график этой функции симметричен относительно оси  . (См. рис. 57)
. (См. рис. 57)
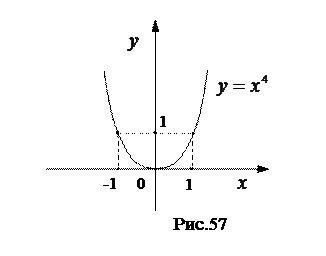
Функция  называется нечетной, если
называется нечетной, если 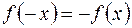 . График нечетной функции симметричен относительно начала координат.
. График нечетной функции симметричен относительно начала координат.
Пример. Функция 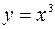 является нечетной, так как
является нечетной, так как 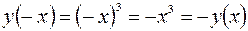 , следовательно, график этой функции симметричен относительно начала координат. (См. рис. 58)
, следовательно, график этой функции симметричен относительно начала координат. (См. рис. 58)
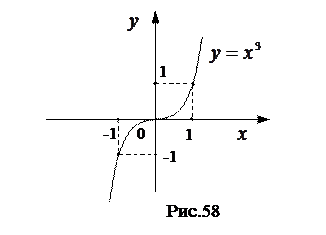
Заметим, что график четной (нечетной) функции достаточно исследовать только при 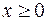 , а при
, а при 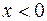 достроить по симметрии, то есть симметрично относительно оси
достроить по симметрии, то есть симметрично относительно оси 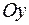 (начала координат).
(начала координат).
Функция  называется периодической, если существует такое положительное число
называется периодической, если существует такое положительное число 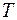 , что
, что 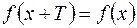 . Наименьшее из таких чисел
. Наименьшее из таких чисел 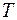 называется периодом функции. График периодической функции достаточно построить на отрезке оси
называется периодом функции. График периодической функции достаточно построить на отрезке оси 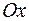 длины периода
длины периода 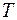 , а затем продолжить, сдвигая на
, а затем продолжить, сдвигая на 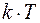 , где
, где 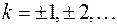 по оси
по оси 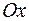 .
.
Пример. Функция 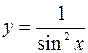 периодическая с периодом
периодическая с периодом 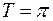 , так как
, так как 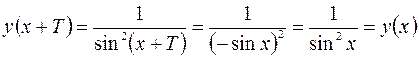 . График этой функции изображен на рис. 59.
. График этой функции изображен на рис. 59.
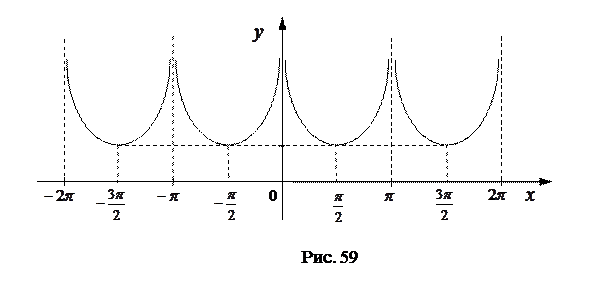
 2015-03-22
2015-03-22 8541
8541
