Функция  называется возрастающей (убывающей) на интервале
называется возрастающей (убывающей) на интервале 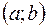 , если для любых точек
, если для любых точек 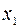 ,
, 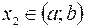 таких, что
таких, что 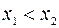 , имеет место неравенство:
, имеет место неравенство: 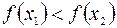
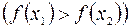 .
.
Дифференцируемая на интервале 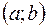 функция
функция  возрастает (убывает) на интервале
возрастает (убывает) на интервале 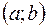 , тогда и только тогда, когда для любого
, тогда и только тогда, когда для любого 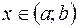 :
: 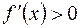
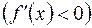 .
.
Точка  называется точкой максимума (минимума) функции
называется точкой максимума (минимума) функции  , если:
, если:
1) функция  определена в некоторой
определена в некоторой 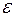 - окрестности точки
- окрестности точки  ;
;
2) для любого 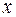 из
из 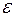 - окрестности точки
- окрестности точки  справедливо неравенство:
справедливо неравенство: 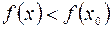
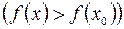 (См. рис. 60 и 61).
(См. рис. 60 и 61).
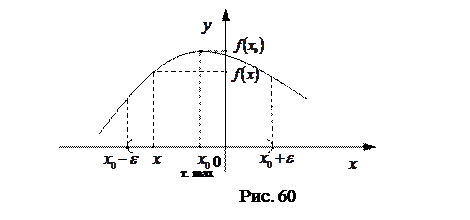
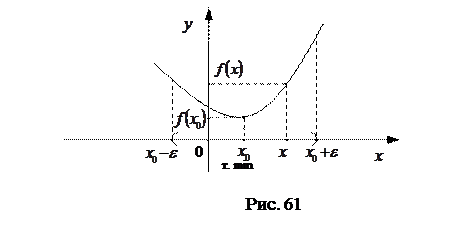
Точкимаксимума и минимума функции называются точками экстремума функции.
Необходимое условие экстремума: если  – точка экстремума функции
– точка экстремума функции  , то в этой точке либо
, то в этой точке либо 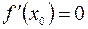 , либо производная не существует.
, либо производная не существует.
Достаточные условия экстремума: пусть функция  дифференцируема и непрерывна в
дифференцируема и непрерывна в 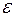 – окрестности критической точки
– окрестности критической точки  кроме, быть может, самой точки
кроме, быть может, самой точки  , тогда, если ее первая производная меняет знак минус на плюс (плюс на минус) при переходе через точку
, тогда, если ее первая производная меняет знак минус на плюс (плюс на минус) при переходе через точку  , то
, то  – точка максимума (минимума) функции
– точка максимума (минимума) функции  .
.
Пример. Найти интервалы монотонности и точки экстремума функции 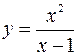 .
.
Решение. Областью определения 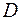 данной функции
данной функции  является вся числовая ось
является вся числовая ось 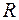 , кроме точки
, кроме точки 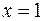 , то есть
, то есть 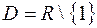 .
.
Находим первую производную:
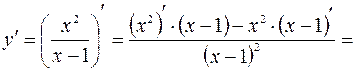
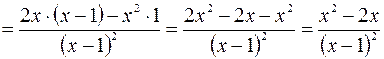 .
.
Используя необходимые условия экстремума, находим критические точки:
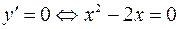 или
или 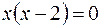 , откуда
, откуда 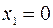 или
или 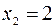 .
.
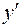 не существует
не существует 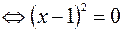 , откуда
, откуда 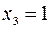 .
.
Используем достаточные условия экстремума. Наносим три критические точки 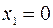 ;
; 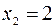 ;
; 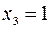 на область определения
на область определения 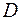 функции
функции  . Они разбивают область
. Они разбивают область 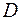 на четыре интервала. Определяем знак функции
на четыре интервала. Определяем знак функции 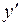 в каждом интервале.
в каждом интервале.

Так как 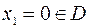 и при переходе через эту точку
и при переходе через эту точку 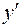 меняет знак плюс на минус, то
меняет знак плюс на минус, то 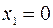 – точка максимума функции
– точка максимума функции  .
.
Так как 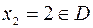 и при переходе через эту точку
и при переходе через эту точку 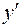 меняет знак минус на плюс, то
меняет знак минус на плюс, то 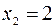 – точка минимума функции
– точка минимума функции  .
.
Так как при любом 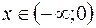 или
или 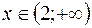
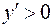 , то в интервалах
, то в интервалах 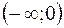 и
и 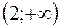 функция
функция  монотонно возрастает.
монотонно возрастает.
Так как при любом 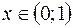 или
или 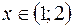
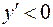 , то в интервалах
, то в интервалах 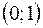 и
и 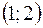 функция
функция  монотонно убывает.
монотонно убывает.
 2015-03-22
2015-03-22 955
955








