2015-03-22
3657
График функции 
называется выпуклым вниз в интервале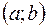 
, если он расположен ниже касательной, проведенной в любой точке 
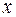этого интервала (См. рис. 62).
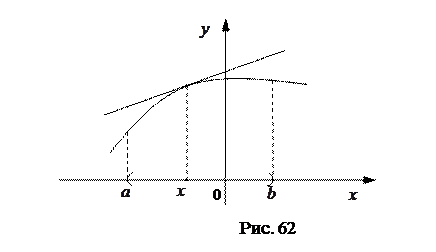
График функции называется выпуклым вверх в интервале 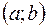, если он расположен выше касательной, проведенной в любой точке 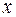этого интервала (См. рис. 63).
Достаточное условие выпуклости (вогнутости) графика функции:
если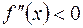 
в интервале 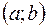, то график функции является выпуклым вниз в этом интервале; если же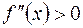 
, то в интервале 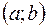график функции – выпуклый вверх.
Пусть функция дифференцируема в интервале 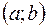и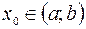 
. Точку 
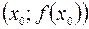графика функции называют точкой перегиба этого графика, если существует такая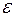 
– окрестность точки 
оси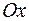 
, в границах которой график функции слева и справа от точки имеет разные направления выпуклости (См. рис. 64).
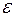Необходимое условие перегиба функции в точке : если – точка перегиба функции и функция имеет в некоторой – окрестности точки вторую производную, непрерывную в точке , то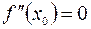 
.
Достаточное условие перегиба функции в точке : если функция непрерывна в 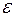– окрестности точки , имеет в точке конечную или бесконечную определенного знака производную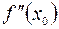 
, а функция 
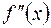определена в 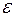– окрестности точки , кроме быть может самой точки , и меняет знак при переходе через эту точку, то – точка перегиба функции .
Пример. Найти интервалы выпуклости (вогнутости) и точки перегиба функции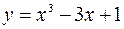 
.
Решение. Область определения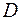 
данной функции есть множество всех действительных чисел 
, то есть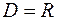 
.
Находим:
;
.
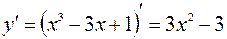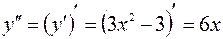Используя необходимое условие перегиба, находим:
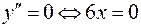, откуда 
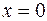– точка «подозрительная» на точку перегиба.
Используем достаточные условия перегиба:
Отметим точку 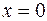на области 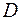и определим знаки 
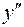слева и справа от точки .
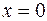Так как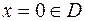 
и при переходе через эту точку 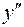меняет знак, то 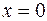– точка перегиба данной функции.
Так как для любого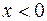 
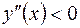, то в интервале 
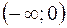функция 
выпукла вниз.
Так как для любого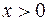 
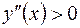, то в интервале 
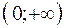функция выпукла вверх.
