Если на множестве Х функции 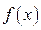 и
и 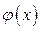 одновременно возрастают или убывают, то
одновременно возрастают или убывают, то 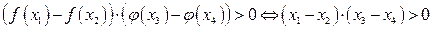 .
.
Если на множестве Х одна из функций 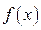 или
или 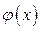 возрастает, а другая убывает, то
возрастает, а другая убывает, то 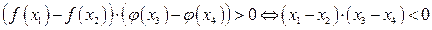 .
.
1. Пусть 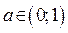 . Так как функция
. Так как функция 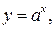 если
если 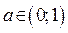 , убывает, а функция
, убывает, а функция 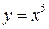 возрастает, то
возрастает, то 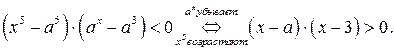
Так как неравенство 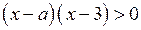 квадратное, коэффициент при
квадратное, коэффициент при 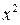 положительный и
положительный и 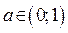 , то множеством решений этого неравенства является множество
, то множеством решений этого неравенства является множество 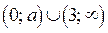 , где
, где 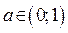 . Это множество содержит более трёх целых чисел.
. Это множество содержит более трёх целых чисел.
2. Пусть 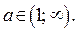 Так как функции
Так как функции 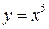 ,
, 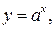 если
если 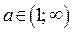 , возрастают, то
, возрастают, то 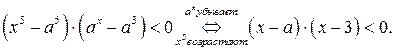
Рассмотрим неравенство
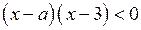 , где
, где 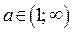 ,
, 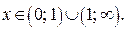 (3)
(3)
1) Пусть 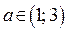 . Множеством решений неравенства (3) является интервал
. Множеством решений неравенства (3) является интервал 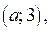 где
где 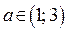 , который ни при каких значениях
, который ни при каких значениях 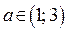 не содержит ровно трёх целых чисел.
не содержит ровно трёх целых чисел.
2) Пусть 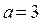 . Тогда неравенство (3) принимает вид
. Тогда неравенство (3) принимает вид 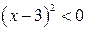 , так как последнее неравенство не имеет решений, то
, так как последнее неравенство не имеет решений, то 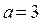 не удовлетворяет условию задачи.
не удовлетворяет условию задачи.
3) Пусть 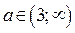 . Множеством решений неравенства (3) является интервал
. Множеством решений неравенства (3) является интервал 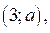 где
где 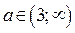 . Интервал
. Интервал 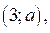 где
где 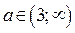 , содержит ровно три целых числа (это числа: 4, 5, 6), если
, содержит ровно три целых числа (это числа: 4, 5, 6), если 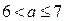 .
.
Ответ. 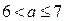 .
.
35. Найдите все значения параметра а, при каждом из которых неравенство 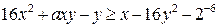 (1) выполняется для любых пар чисел
(1) выполняется для любых пар чисел 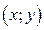 таких, что
таких, что 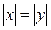 .
.
Решение. Имеем 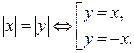
Если 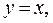 то неравенство (1)принимает вид
то неравенство (1)принимает вид
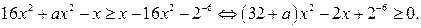
Если 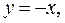 то неравенство (1)принимает вид
то неравенство (1)принимает вид
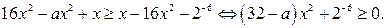
Рассмотрим систему 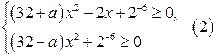
Отметим: если система неравенств (2) выполняется для любых значений х при некотором значении параметра 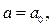 то неравенство (1)выполняется для любых пар чисел
то неравенство (1)выполняется для любых пар чисел 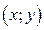 таких, что
таких, что 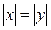 при значении параметра
при значении параметра 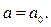
Система неравенств (2) имеет решения при любых значениях х тогда и только тогда, когда 1) в первом неравенстве коэффициент при 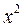 положительный и дискриминант
положительный и дискриминант 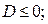 2) во втором неравенстве коэффициент при
2) во втором неравенстве коэффициент при 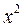 не отрицательный, то есть, если
не отрицательный, то есть, если
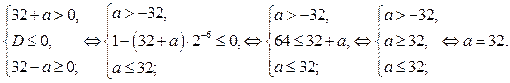
Система (2) выполняется для любых значений х, если 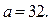
Ответ. 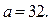 .
.
36. Найдите все значения параметра а, при которых каждое решение неравенства 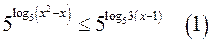 является решением неравенства
является решением неравенства 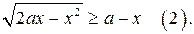
Решение. 1. Найдём решение неравенства (1).
Неравенство (1) равносильно системе
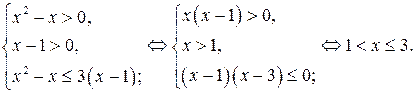
Итак, решениями неравенства (1) являются 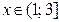 .
.
2. Так как надо найдите все значения параметра а, при которых каждое 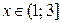 является решением неравенства (2), то рассмотрим это неравенства при
является решением неравенства (2), то рассмотрим это неравенства при 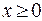 .
.
2. Рассмотрим неравенство (2) при различных значениях параметра а.
1) Если 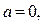 то ОДЗ неравенства:
то ОДЗ неравенства: 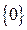 (находим из неравенства
(находим из неравенства 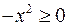 ). Параметр
). Параметр 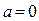 не удовлетворяет условию задачи.
не удовлетворяет условию задачи.
2) Если 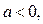 то ОДЗ неравенства:
то ОДЗ неравенства: 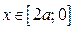 (находим из неравенства
(находим из неравенства 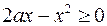 ). Параметр
). Параметр 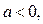 не удовлетворяет условию задачи.
не удовлетворяет условию задачи.
3) Если 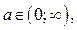 то ОДЗ неравенства:
то ОДЗ неравенства: 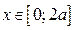 (находим из неравенства
(находим из неравенства 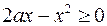 ).
).
Рассмотрим функции 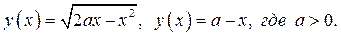 .
.
Имеем
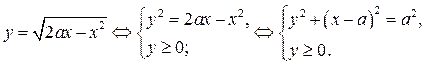
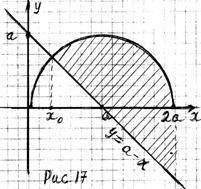 Графиком функции
Графиком функции 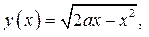
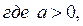 является полуокружности, расположенная над осью абсцисс, с центром в точке (а; 0) и радиусом, равным а. На координатной плоскости х0у построим графики функций
является полуокружности, расположенная над осью абсцисс, с центром в точке (а; 0) и радиусом, равным а. На координатной плоскости х0у построим графики функций 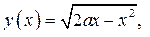
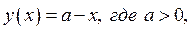 при некотором значении а. Отметим: прямая
при некотором значении а. Отметим: прямая 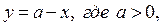 проходит через точку (а; 0) – центр окружности.
проходит через точку (а; 0) – центр окружности.
Из рисунка 17 следует: если 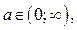 то решением неравенства (2) является отрезок
то решением неравенства (2) является отрезок 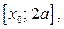 где
где 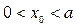 . Абсциссу
. Абсциссу 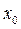 точки пересечения графиков функций
точки пересечения графиков функций 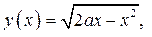
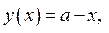
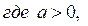
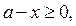 найдём из системы
найдём из системы
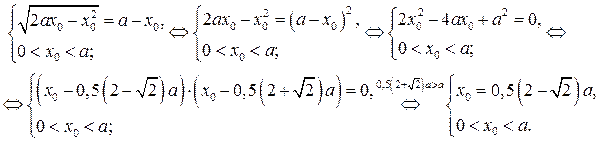 Итак, решениями неравенства (2) являются
Итак, решениями неравенства (2) являются 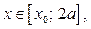 где
где 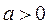 и
и 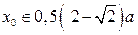 .
.
2) Промежуток 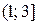 является решением неравенства (2) при тех значениях параметра
является решением неравенства (2) при тех значениях параметра 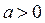 , при которых
, при которых 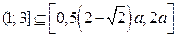 . Значения параметра
. Значения параметра 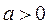 найдём из системы
найдём из системы
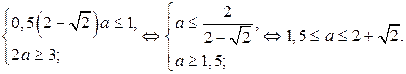
Из последней системы следует ответ.
Ответ. 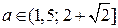 .
.
Замечание. График уравнения 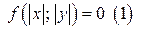 симметричен относительно осей координат. Для построения графика уравнения (1) надо построить график уравнения
симметричен относительно осей координат. Для построения графика уравнения (1) надо построить график уравнения 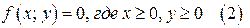 . График уравнения (1) получается симметричным отображением относительно осей координат графика уравнения (2) (каждая точка
. График уравнения (1) получается симметричным отображением относительно осей координат графика уравнения (2) (каждая точка 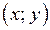 графика уравнения (2) переходит в точки
графика уравнения (2) переходит в точки 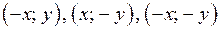 )
)
37. Найдите все значения параметра а, при которых количество целых чисел 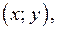 удовлетворяющих неравенству
удовлетворяющих неравенству 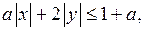 минимально.
минимально.
Решение. Для построения графика неравенства 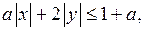 надо
надо
1) построить график уравнения 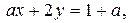 где
где 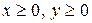 (*);
(*);
2) симметричным отображением относительно осей координат графика уравнения (*) построить график уравнения 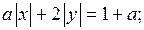
 3) изобразить на координатной плоскости множество точек, удовлетворяющих неравенству
3) изобразить на координатной плоскости множество точек, удовлетворяющих неравенству 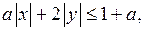 (берём любую точку плоскости
(берём любую точку плоскости 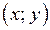 и определяем, будет ли она удовлетворять рассматриваемому неравенству, затем воспользуемся замечанием на стр. 2).
и определяем, будет ли она удовлетворять рассматриваемому неравенству, затем воспользуемся замечанием на стр. 2).
 1. Рассмотрим неравенство
1. Рассмотрим неравенство 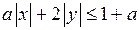 (1) при различных значениях параметра а.
(1) при различных значениях параметра а.
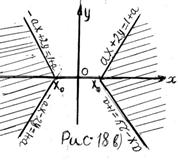
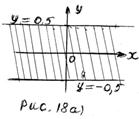
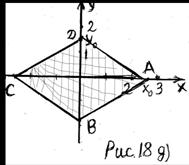
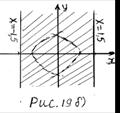
1) Если 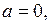 то неравенство (1) принимает вид
то неравенство (1) принимает вид 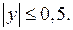 Решением последнего неравенства является полоса (рис. 18 а)), которая содержит бесконечное множество целочисленных точек
Решением последнего неравенства является полоса (рис. 18 а)), которая содержит бесконечное множество целочисленных точек 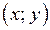 .
.
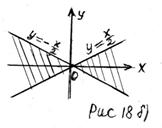 2) Если
2) Если 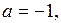 то неравенство (1) принимает вид
то неравенство (1) принимает вид 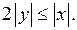 На рисунке 18 б) штриховкой показано множество решений последнего неравенства. Из рисунка 18 б) следует, что множество решений неравенства
На рисунке 18 б) штриховкой показано множество решений последнего неравенства. Из рисунка 18 б) следует, что множество решений неравенства 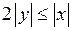 содержит бесконечное множество целочисленных точек
содержит бесконечное множество целочисленных точек 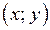 .
.
3) Пусть 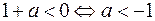 .
.
Построим график неравенства 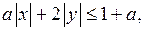 где
где 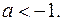 На рисунке 18 в) штриховкой показано множество решений последнего неравенства. Из рисунка 18 в) следует, что множество решений рассматриваемого неравенства содержит бесконечное множество целочисленных точек
На рисунке 18 в) штриховкой показано множество решений последнего неравенства. Из рисунка 18 в) следует, что множество решений рассматриваемого неравенства содержит бесконечное множество целочисленных точек 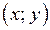 .
.
4) Пусть 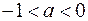 .
.
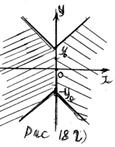 Построим график неравенства
Построим график неравенства 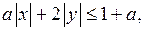 где
где 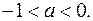 На рисунке 18 г) штриховкой показано множество решений последнего неравенства. Из рисунка 18 г) следует, что множество решений рассматриваемого неравенства содержит бесконечное множество целочисленных точек
На рисунке 18 г) штриховкой показано множество решений последнего неравенства. Из рисунка 18 г) следует, что множество решений рассматриваемого неравенства содержит бесконечное множество целочисленных точек  .
.
5) Пусть 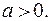
Построим график неравенства 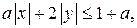 где
где 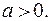 (2)
(2)
Множеством решений неравенства (2) является ромб с вершинами в точках: 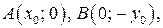
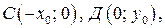 где
где 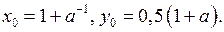
Пусть множеством решений неравенства (2) является множество Х.
2. Рассмотрим неравенство (2) при 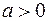 .
.
1) Если 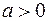 , то
, то 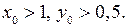 Поэтому для любого
Поэтому для любого 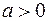 множеству Х принадлежат три целочисленных точки:
множеству Х принадлежат три целочисленных точки: 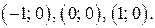 .
.
Множеству Х будут принадлежать три целочисленных точки тогда и только тогда, когда
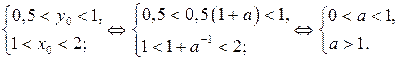
Так как последняя система не имеет решений, то множеству Х принадлежит более трёх целочисленных точек (следует из 1)).
2) Пусть
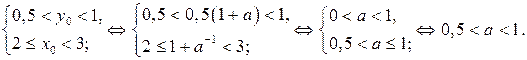
 Если
Если  то множеству Х принадлежит пять целочисленных точек:
то множеству Х принадлежит пять целочисленных точек:
 (рисунок 18 д))
(рисунок 18 д))
3) Пусть
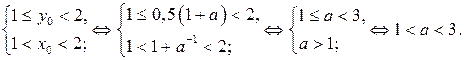
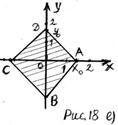 Если
Если 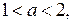 то множеству Х принадлежит пять целочисленных точек:
то множеству Х принадлежит пять целочисленных точек: 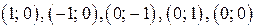 . (рисунок 18 е)) Итак, если
. (рисунок 18 е)) Итак, если 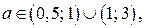 то множеству Х принадлежит пять целочисленных точек. При других значениях параметра а множеству Х принадлежит более пяти целочисленных точек.
то множеству Х принадлежит пять целочисленных точек. При других значениях параметра а множеству Х принадлежит более пяти целочисленных точек.
Ответ. 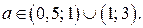
38. Найдите все значения параметра а, при которых множество точек, заданное неравенством 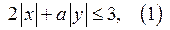 является подмножеством множество точек, заданное неравенством
является подмножеством множество точек, заданное неравенством 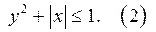
Решение. Пусть множество решений неравенства (1) есть множество 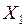 , а неравенства (2) –
, а неравенства (2) – 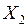 . Надо найти все значения параметра а, при которых
. Надо найти все значения параметра а, при которых 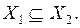
1. Рассмотрим неравенство (2). Имеем
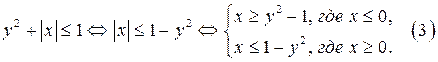
Построим график системы (3).
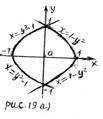 1) Графиком функции
1) Графиком функции 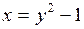 , где
, где 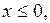 является часть параболы, с вершиной в точке
является часть параболы, с вершиной в точке 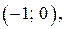 осью симметрии которой является ось абсцисс и ветви направлены вправо.
осью симметрии которой является ось абсцисс и ветви направлены вправо.
2) Графиком функции 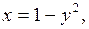 где
где 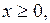 является часть параболы, с вершиной в точке
является часть параболы, с вершиной в точке 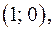 осью симметрии которой является ось абсцисс и ветви направлены влево.
осью симметрии которой является ось абсцисс и ветви направлены влево.
3) График системы (3) (график множества 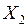 ) изображён на рисунке (19 а)) штриховкой, граница области принадлежит графику системы.
) изображён на рисунке (19 а)) штриховкой, граница области принадлежит графику системы.
 2. Рассмотрим неравенство
2. Рассмотрим неравенство 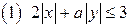 при различных значениях параметра а.
при различных значениях параметра а.
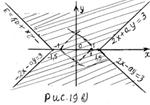
1) Если 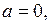 то неравенство (1) принимает вид
то неравенство (1) принимает вид 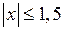 . Решением последнего неравенства (множество
. Решением последнего неравенства (множество 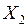 ) является полоса (рис. 19 б)), которая содержит множество
) является полоса (рис. 19 б)), которая содержит множество 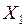 . Параметр
. Параметр 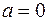 удовлетворяет условию задачи.
удовлетворяет условию задачи.
 2) Пусть
2) Пусть  .
.
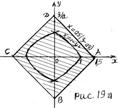 График неравенства
График неравенства  , где
, где 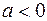 , изображён штриховкой на рисунке 19 в). Из рисунка 19 в) следует, что множество решений рассматриваемого неравенства (множество
, изображён штриховкой на рисунке 19 в). Из рисунка 19 в) следует, что множество решений рассматриваемого неравенства (множество 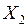 ) содержит множество
) содержит множество 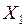 . Параметр
. Параметр 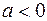 удовлетворяет условию задачи.
удовлетворяет условию задачи.
3) Пусть 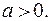
Построим график неравенства 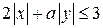 , где
, где 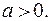
На рисунке 19 г) штриховкой показано множество решений последнего неравенства (множество 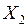 ). Множеством решений неравенства (2) является ромб с вершинами в точках:
). Множеством решений неравенства (2) является ромб с вершинами в точках: 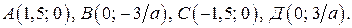
Рассмотрим, при каких значениях параметра а ромб содержит множество 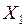 (т.е.
(т.е. 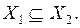 ) Так как графики каждого неравенства (1) и (2) симметричны относительно осей координат, то рассмотрим эти неравенства при
) Так как графики каждого неравенства (1) и (2) симметричны относительно осей координат, то рассмотрим эти неравенства при 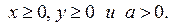 В этом случае неравенства (1) и (2) соответственно принимают вид:
В этом случае неравенства (1) и (2) соответственно принимают вид: 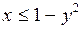 и
и 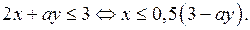
Если графики функций 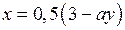 и
и 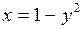 пересекаются не более, чем в одной точке, то
пересекаются не более, чем в одной точке, то 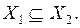
Графики функций 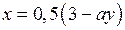 и
и 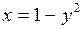 пересекаются не более чем в одной точке, если имеет не более одного решения уравнение
пересекаются не более чем в одной точке, если имеет не более одного решения уравнение
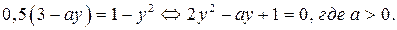 (4)
(4)
Пусть D дискриминант квадратного уравнения (4). Уравнение имеет не более одного решения, если
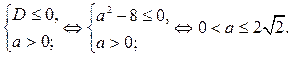
Итак, если 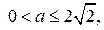 то
то 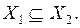 Это означает, что
Это означает, что 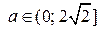 удовлетворяют условию задачи.
удовлетворяют условию задачи.
Из 1) – 3) следует ответ.
Ответ. 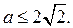
 2015-03-22
2015-03-22 393
393








