Общие сведения. 1. При решении неравенств с модулем пользуемся тем, что

Задачи с параметрами

Неравенства.

задачи типа заданий С 5

Дихтярь М.Б.

Общие сведения

1. При решении неравенств с модулем пользуемся тем, что

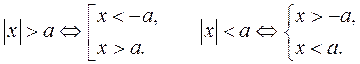
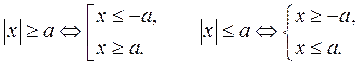
2. Изобразить на координатной плоскости множество решений неравенства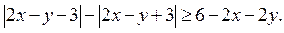

Решение. Перепишем исходное неравенство в виде

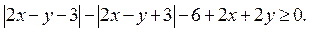(1)

На координатной плоскости 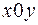построим график уравнения

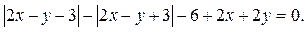(2)

Для построения множества точек, удовлетворяющих уравнению (2), проделаем следующее.

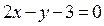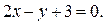1. Приравняем нулю выражения, стоящие под знаком модуля: и Построим прямые 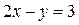и 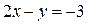(прямые параллельны). Эти прямые разобьют плоскость 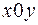на 3 области.

2. Рассмотрим уравнение (2) в каждой области. Для этого раскроем модули в каждой области.

Замечание. При раскрытии модулей надо учитывать знак выражения, стоящего под модулем в соответствующей области. Так как знак в каждой области постоянный, то знак выражения в области совпадает со знаком выражения в любой точке этой области.

1) В области I уравнение (2) равносильно системе

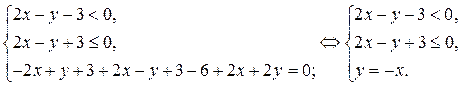
Для построение в области I части прямой 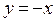, найдём точку пересечения прямых 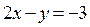(граница области) и 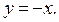Имеем

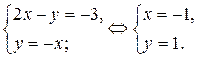
В области I строим часть прямой 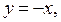которая в этой области проходит через точку А (–1; 1).

2) В области II уравнение (2) равносильно системе

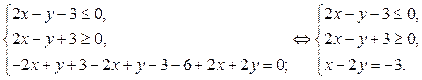
Найдём точку пересечения прямых 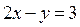(граница области) и 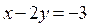. Имеем

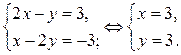
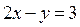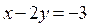Точкой пересечения прямых и является точка В (3; 3).

Легко проверить, что точкой пересечения прямых 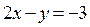(граница области) и 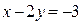является точка А (–1; 1).

В области II строим часть прямой 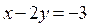, которая в этой области проходит через точки А (–1; 1) и В (3; 3).

3) В области III уравнение (2) равносильно системе

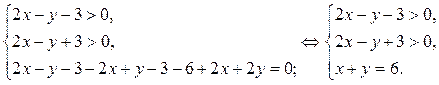
В области III строим часть прямой 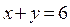, которая в этой области проходит через точки В (3; 3) и С (6; 0).

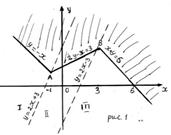
3. Ломаная линия (рис. 1) разбивает плоскость х0у на две части, в каждой из которых функция 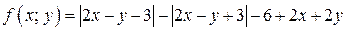(левая часть неравенства (1)) сохраняет знак.

Замечание. Прямая 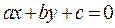разбивает координатную плоскость на две области, в каждой из которых функция 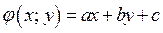сохраняет знак.

Определим знак функции 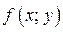в точке (0; 0). Так как 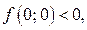то 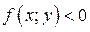в области расположенной ниже ломаной, 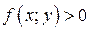в области расположенной выше ломаной и 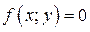в точках, принадлежащих ломаной.

Решением исходного неравенства является множество точек, расположенных выше ломаной, включая ломаную. Множество решений исходного неравенства изображено на рисунке 1 штриховкой (граница области принадлежит множеству решений исходного неравенства).

3. Изобразить на координатной плоскости множество решений неравенства .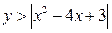

Решения. На координатной плоскости 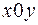построим график функции .

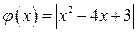Имеем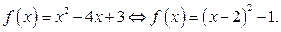

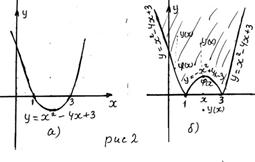
Из последнего уравнения следует, что графиком функции 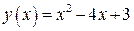является парабола с вершиной в точке (2; –1), ветви которой направлены вверх.

Точки пересечения параболы 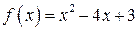с осью абсцисс находим из уравнения

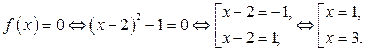
Строим график параболы 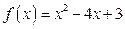(рис. 2 а)). Строим график функции 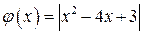(рис. 2 б)).

Любая точка, принадлежащая графику функции 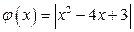, имеет координаты 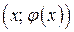, а точка, не принадлежащая этому графику, имеет координаты 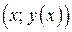. Решением исходного неравенства является множество точек, удовлетворяющих неравенству 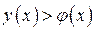. Множество решений изображено на рисунке 2б) штриховкой (граница области не принадлежит множеству решений неравенства).