5. Решите неравенство 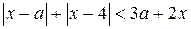 . (1)
. (1)
Решение. На координатной плоскости х0а построим множество точек,
удовлетворяющих уравнению 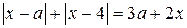 . (1)
. (1)
Для построения множества точек, удовлетворяющих уравнению (1) проделаем следующее.
1. Приравняем нулю выражения, стоящие под знаком модуля: 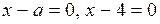 . Построим прямые
. Построим прямые 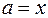 и
и 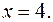 . Эти прямые разобьют координатную плоскость х0а на 4 области.
. Эти прямые разобьют координатную плоскость х0а на 4 области.
2. Рассмотрим уравнение (1) в каждой области и построим в каждой области соответствующее множество точек.
1) В области I уравнение (1) равносильно системе
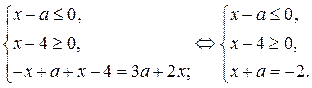
В области I не существует точек, принадлежащих прямой 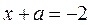 (так как
(так как 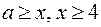 ).
).
2) В области II уравнение (1) равносильно системе
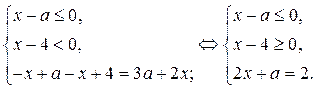
Из последнего уравнения системы следует, что 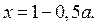
В области II строим часть прямой 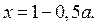 Для этого найдём точки пересечения прямой
Для этого найдём точки пересечения прямой 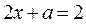 с границей области:
с границей области: 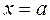 и
и 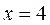 .
.
а) Точки пересечении прямых 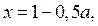
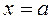 найдём из системы
найдём из системы
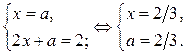
Точки 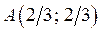 принадлежит области II.
принадлежит области II.
б) Точкой пересечении прямых 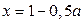 и
и 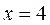 является точка
является точка 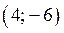 , которая не принадлежит области II.
, которая не принадлежит области II.
Очевидно, прямая 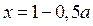 проходит через точку
проходит через точку 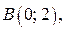 которая принадлежит области II.
которая принадлежит области II.
Через точки 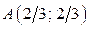 и
и 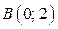 в области II строим часть прямой
в области II строим часть прямой 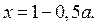
3) В области III уравнение (1) равносильно системе
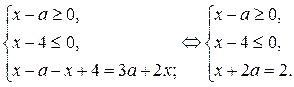
Из последнего уравнения системы следует, что 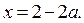
В области III строим часть прямой 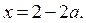
Точка 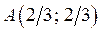 является точкой пересечения прямых
является точкой пересечения прямых 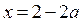 и
и 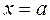 . Точка
. Точка 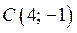 является точкой пересечения прямых
является точкой пересечения прямых 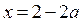 и
и 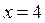 . Через точки
. Через точки 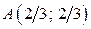 и
и 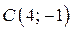 в области III строим часть прямой
в области III строим часть прямой 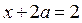 .
.
3) В области IV уравнение (1) равносильно системе
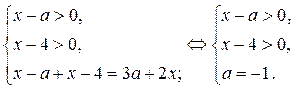
В области IV строим часть прямой 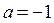 .
.
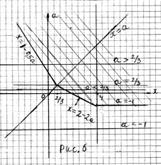
3. Дляопределения области, каждая точка которой принадлежит множеству решений неравенства 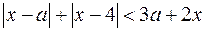 , возьмём любую точку плоскости х0а, например, точка (0; 0) и определим, удовлетворяет ли она исходному неравенству. Так как точка (0; 0) не удовлетворяет исходному неравенству, то множеством решений исходного неравенства является область, которой не принадлежит точка (0; 0). (Воспользовались замечанием на стр. 2.) Заштрихованная область, в которую не входит граница области (рисунок 6), соответствует множеству решений исходного неравенства.
, возьмём любую точку плоскости х0а, например, точка (0; 0) и определим, удовлетворяет ли она исходному неравенству. Так как точка (0; 0) не удовлетворяет исходному неравенству, то множеством решений исходного неравенства является область, которой не принадлежит точка (0; 0). (Воспользовались замечанием на стр. 2.) Заштрихованная область, в которую не входит граница области (рисунок 6), соответствует множеству решений исходного неравенства.
Для того чтобы найти решения исходного неравенства, проведём прямые 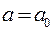 .
.
Замечание. Если прямая 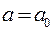 не принадлежат заштрихованной области, то исходное неравенство при
не принадлежат заштрихованной области, то исходное неравенство при 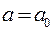 не имеет решений.
не имеет решений.
Если прямая 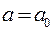 пересекает границу заштрихованной области в точке с абсциссой
пересекает границу заштрихованной области в точке с абсциссой 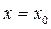 , то решениями исходного неравенства при
, то решениями исходного неравенства при 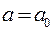 являются
являются 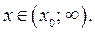 .
.
Из рисунка 6 и замечания следует ответ.
Ответ. Если 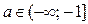 , то нет решений; если
, то нет решений; если 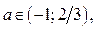 , то
, то 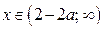 ; если
; если 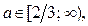 то
то 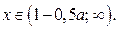
6. Решите неравенство 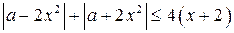 .
.
Решение. На координатной плоскости х0а построим множество точек, удовлетворяющих уравнению 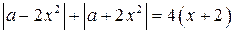 . (1)
. (1)
Для построения множества точек, удовлетворяющих уравнению (1), проделаем следующее.
1. Приравняем нулю выражения, стоящие под знаком модуля: 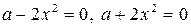 . Построим параболы
. Построим параболы 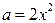 и
и 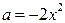 . Эти параболы разобьют координатную плоскость х0а на 3 области.
. Эти параболы разобьют координатную плоскость х0а на 3 области.
2. Рассмотрим уравнение (1) в каждой области и построим в каждой области соответствующее множество точек.
В области I уравнение (1) равносильно системе
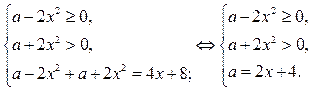
В области I строим часть прямой 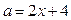 .
.
Найдём точки пересечении прямой 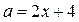 и параболы
и параболы 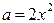 (граница области) из системы
(граница области) из системы
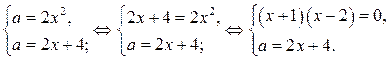
Точки 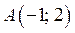 и
и 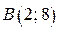 являются решениями последней системы. Через эти точки в области I строим часть прямой
являются решениями последней системы. Через эти точки в области I строим часть прямой 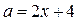 . Из последнего уравнения следует, что
. Из последнего уравнения следует, что 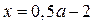 .
.
В области II уравнение (1) равносильно системе
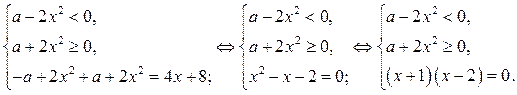
Графиком уравнения 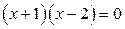 является совокупность прямых
является совокупность прямых 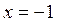 и
и 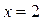 . Прямая
. Прямая 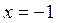 в области II проходит через точки
в области II проходит через точки 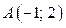 и
и 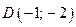 (точки пересечения прямой
(точки пересечения прямой 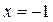 с границей области). Прямая
с границей области). Прямая 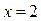 в области II проходит через точки
в области II проходит через точки 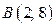 и
и 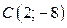 (точки пересечения прямой
(точки пересечения прямой 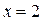 с границей области).
с границей области).
В области III уравнение (1) равносильно системе
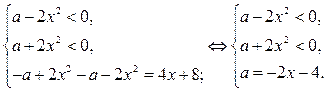
В области III строим часть прямой 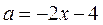 . Для этого найдём точки пересечении прямой
. Для этого найдём точки пересечении прямой 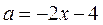 и параболы
и параболы 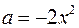 (граница области) из системы
(граница области) из системы
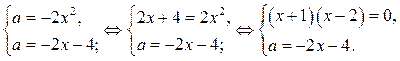
Точки 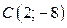 и
и 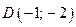 являются решениями последней системы. Через эти точки в области III строим часть прямой
являются решениями последней системы. Через эти точки в области III строим часть прямой 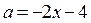 . Из последнего уравнения следует, что
. Из последнего уравнения следует, что 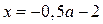 .
.
 Дляопределения области, каждая точка которой принадлежит множеству решений неравенства
Дляопределения области, каждая точка которой принадлежит множеству решений неравенства 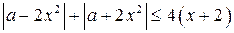 , возьмём любую точку плоскости х0а, например, точка (0; 1) и определим, удовлетворяет ли она исходному неравенству. Так как точка (0; 1) удовлетворяет исходному неравенству, то множеством решений исходного неравенства является область, которой принадлежит точка (0; 1). (Воспользовались замечанием на стр. 2.)
, возьмём любую точку плоскости х0а, например, точка (0; 1) и определим, удовлетворяет ли она исходному неравенству. Так как точка (0; 1) удовлетворяет исходному неравенству, то множеством решений исходного неравенства является область, которой принадлежит точка (0; 1). (Воспользовались замечанием на стр. 2.)
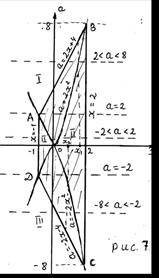
Заштрихованная область, в которую входит граница области (рисунок 7), соответствует множеству решений исходного неравенства.
Для того чтобы найти решения исходного неравенства, проведём прямые 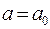 .
.
Замечание. Если прямая 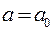 не принадлежат заштрихованной области, то исходное неравенство при
не принадлежат заштрихованной области, то исходное неравенство при 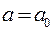 не имеет решений.
не имеет решений.
Если прямая 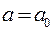 пересекает границу заштрихованной области в точках с абсциссами
пересекает границу заштрихованной области в точках с абсциссами 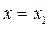 и
и 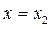 , то решениями исходного неравенства при
, то решениями исходного неравенства при 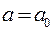 являются
являются 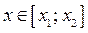 .
.
Если прямая 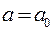 пересекает границу заштрихованной области в одной точке с абсциссой
пересекает границу заштрихованной области в одной точке с абсциссой 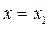 , то исходное неравенство при
, то исходное неравенство при 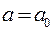 имеет единственное решение
имеет единственное решение 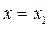 .
.
Из рисунка 7 и замечания следует ответ.
Ответ. Если 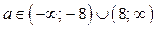 ,то решений нет; если
,то решений нет; если 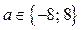 , то
, то 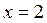 ; если
; если 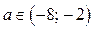 ,то
,то 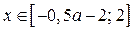 ; если
; если 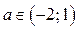 , то
, то 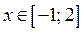 ; если
; если 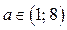 , то
, то 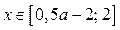 .
.
 2015-03-22
2015-03-22 805
805








